Light travel time delay#
import exoplanet
exoplanet.utils.docs_setup()
print(f"exoplanet.__version__ = '{exoplanet.__version__}'")
WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.
exoplanet.__version__ = '0.6.0'
A simple example showing the effects of light travel time delay on an edge-on planet in an orbit similar to that of Earth.
import matplotlib.pyplot as plt
import numpy as np
from astropy import units as u
import exoplanet as xo
Let’s instantiate an orbit corresponding to a massless Earth orbiting the Sun in a circular orbit, viewed edge-on:
orbit = xo.orbits.KeplerianOrbit(
period=365.25,
t0=0.0,
incl=0.5 * np.pi,
ecc=0.0,
omega=0.0,
Omega=0.0,
m_planet=0.0,
m_star=1.0,
r_star=1.0,
)
In the observer’s coordinate system, the Earth will be seen to transit the Sun when its x position is zero. We specified the reference transit time to be t0 = 0, so let’s check that this is indeed the case. Below we compute the time closest to the point where x = 0:
t = np.linspace(-0.01, 0.01, 9999)
x, y, z = orbit.get_planet_position(t)
t0_obs1 = t[np.argmin(np.abs(x.eval()))]
print("{:.4f}".format(t0_obs1))
0.0000
No surprises here! But what happens if we add light travel time delay into the mix?
x, y, z = orbit.get_planet_position(t, light_delay=True)
t0_obs2 = t[np.argmin(np.abs(x.eval()))]
print("{:.4f}".format(t0_obs2))
-0.0058
Recall that the time is in days by default. Let’s see what it is in minutes:
print("{:.2f}".format((t0_obs2 * u.day).to(u.minute)))
-8.32 min
So when we account for light travel time delay, the Earth appears to transit the Sun early by about 8.3 minutes. In exoplanet, the reference time t0 is specified relative to the origin of the coordinate system (in this case, the position of the Sun). You can check that this is in fact the light travel time from the Sun to the Earth.
Since transits happen early, you might guess that the opposite is true for secondary eclipses: they appear to occur late. Let’s check this. Absent any time delay, the center of the eclipse should again occur when x = 0, half a period after the transit:
t = np.linspace(
0.5 * orbit.period.eval() - 0.01, 0.5 * orbit.period.eval() + 0.01, 9999
)
x, y, z = orbit.get_planet_position(t)
t0_obs1 = t[np.argmin(np.abs(x.eval()))]
print("{:.4f}".format(t0_obs1))
182.6250
x, y, z = orbit.get_planet_position(t, light_delay=True)
t0_obs2 = t[np.argmin(np.abs(x.eval()))]
print("{:.4f}".format(t0_obs2))
182.6308
The difference between those two is
print("{:.2f}".format(((t0_obs2 - t0_obs1) * u.day).to(u.minute)))
8.32 min
as expected.
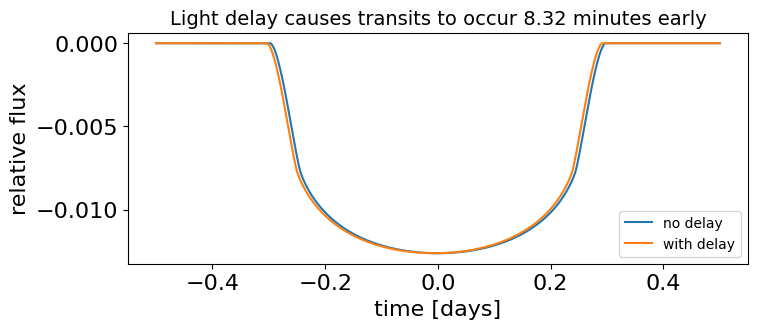
As an example, here’s a comparison between a transit light curve that includes light travel delay and one that doesnt’t:
# Region around transit
t = np.linspace(-0.5, 0.5, 20000)
# No light delay
light_curve1 = (
xo.LimbDarkLightCurve(0.5, 0.25)
.get_light_curve(orbit=orbit, r=0.1, t=t)
.eval()
)
# With light delay
light_curve2 = (
xo.LimbDarkLightCurve(0.5, 0.25)
.get_light_curve(orbit=orbit, r=0.1, t=t, light_delay=True)
.eval()
)
# Plot!
fig = plt.figure(figsize=(8, 3))
plt.plot(t, light_curve1, label="no delay")
plt.plot(t, light_curve2, label="with delay")
plt.xlabel("time [days]")
plt.ylabel("relative flux")
plt.legend(fontsize=10, loc="lower right")
_ = plt.title(
"Light delay causes transits to occur 8.32 minutes early", fontsize=14
)