Note

This tutorial was generated from an IPython notebook that can be downloaded here.

Fitting TESS data

In this tutorial, we will reproduce the fits to the transiting planet in the Pi Mensae system discovered by Huang et al. (2018). The data processing and model are similar to the Case study: K2-24, putting it all together tutorial, but with a few extra bits like aperture selection and de-trending.

To start, we need to download the target pixel file:

import numpy as np
from astropy.io import fits
import matplotlib.pyplot as plt

tpf_url = "https://archive.stsci.edu/missions/tess/tid/s0001/0000/0002/6113/6679/tess2018206045859-s0001-0000000261136679-0120-s_tp.fits"
with fits.open(tpf_url) as hdus:
    tpf = hdus[1].data
    tpf_hdr = hdus[1].header

texp = tpf_hdr["FRAMETIM"] * tpf_hdr["NUM_FRM"]
texp /= 60.0 * 60.0 * 24.0
time = tpf["TIME"]
flux = tpf["FLUX"]
m = np.any(np.isfinite(flux), axis=(1, 2)) & (tpf["QUALITY"] == 0)
ref_time = 0.5 * (np.min(time[m])+np.max(time[m]))
time = np.ascontiguousarray(time[m] - ref_time, dtype=np.float64)
flux = np.ascontiguousarray(flux[m], dtype=np.float64)

mean_img = np.median(flux, axis=0)
plt.imshow(mean_img.T, cmap="gray_r")
plt.title("TESS image of Pi Men")
plt.xticks([])
plt.yticks([]);

Aperture selection

Next, we’ll select an aperture using a hacky method that tries to minimizes the windowed scatter in the lightcurve (something like the CDPP).

from scipy.signal import savgol_filter

# Sort the pixels by median brightness
order = np.argsort(mean_img.flatten())[::-1]

# A function to estimate the windowed scatter in a lightcurve
def estimate_scatter_with_mask(mask):
    f = np.sum(flux[:, mask], axis=-1)
    smooth = savgol_filter(f, 1001, polyorder=5)
    return 1e6 * np.sqrt(np.median((f / smooth - 1)**2))

# Loop over pixels ordered by brightness and add them one-by-one
# to the aperture
masks, scatters = [], []
for i in range(10, 100):
    msk = np.zeros_like(mean_img, dtype=bool)
    msk[np.unravel_index(order[:i], mean_img.shape)] = True
    scatter = estimate_scatter_with_mask(msk)
    masks.append(msk)
    scatters.append(scatter)

# Choose the aperture that minimizes the scatter
pix_mask = masks[np.argmin(scatters)]

# Plot the selected aperture
plt.imshow(mean_img.T, cmap="gray_r")
plt.imshow(pix_mask.T, cmap="Reds", alpha=0.3)
plt.title("selected aperture")
plt.xticks([])
plt.yticks([]);

This aperture produces the following light curve:

plt.figure(figsize=(10, 5))
sap_flux = np.sum(flux[:, pix_mask], axis=-1)
sap_flux = (sap_flux / np.median(sap_flux) - 1) * 1e3
plt.plot(time, sap_flux, "k")
plt.xlabel("time [days]")
plt.ylabel("relative flux [ppt]")
plt.title("raw light curve")
plt.xlim(time.min(), time.max());

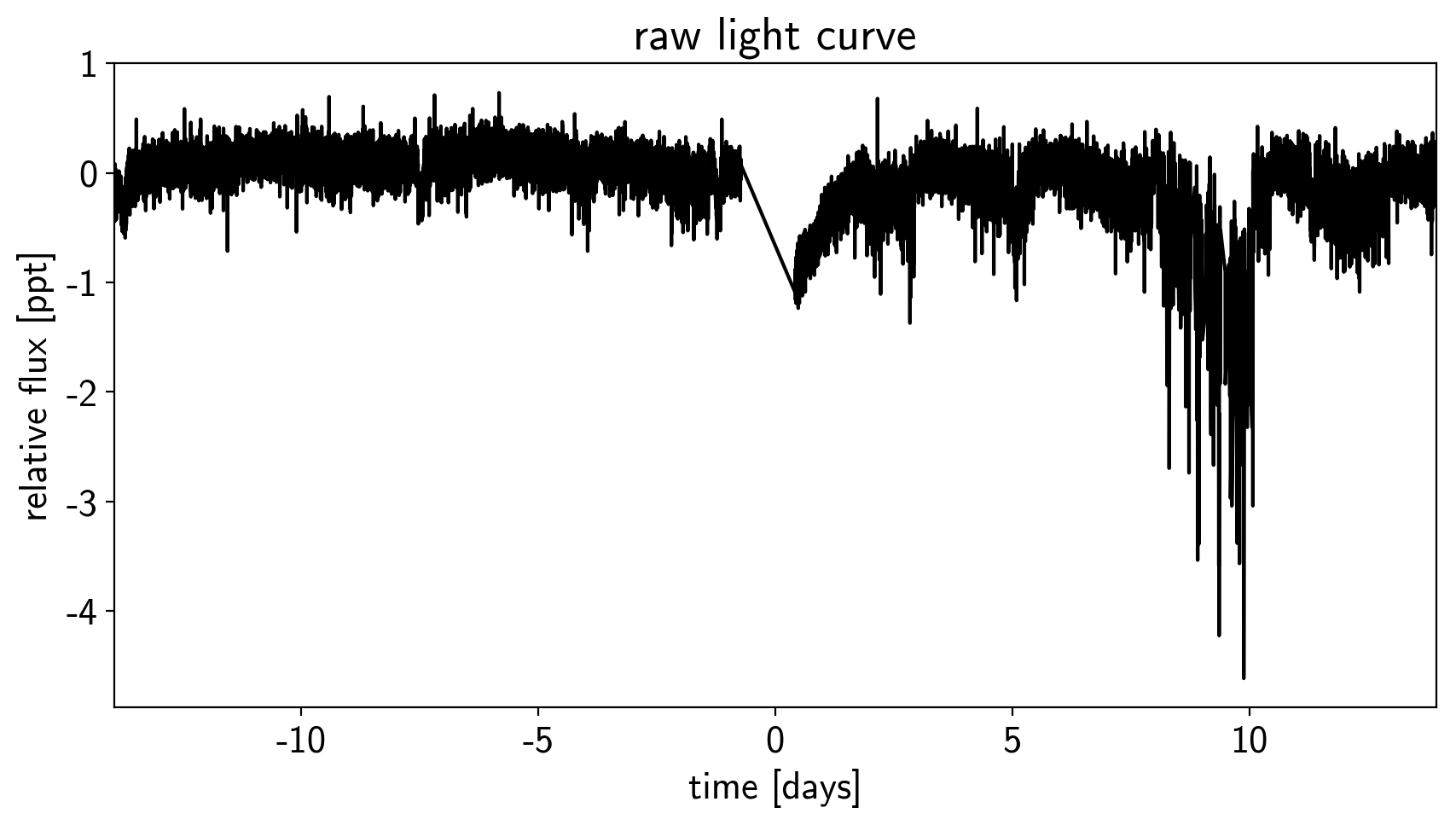
De-trending

This doesn’t look terrible, but we’re still going to want to de-trend it a little bit. We’ll use “pixel-level deconvolution” (PLD) to de-trend following the method used by Everest. Specifically, we’ll use first order PLD plus the top few PCA components of the second order PLD basis.

# Build the first order PLD basis
X_pld = np.reshape(flux[:, pix_mask], (len(flux), -1))
X_pld = X_pld / np.sum(flux[:, pix_mask], axis=-1)[:, None]

# Build the second order PLD basis and run PCA to reduce the number of dimensions
X2_pld = np.reshape(X_pld[:, None, :] * X_pld[:, :, None], (len(flux), -1))
U, _, _ = np.linalg.svd(X2_pld, full_matrices=False)
X2_pld = U[:, :X_pld.shape[1]]

# Construct the design matrix and fit for the PLD model
X_pld = np.concatenate((np.ones((len(flux), 1)), X_pld, X2_pld), axis=-1)
XTX = np.dot(X_pld.T, X_pld)
w_pld = np.linalg.solve(XTX, np.dot(X_pld.T, sap_flux))
pld_flux = np.dot(X_pld, w_pld)

# Plot the de-trended light curve
plt.figure(figsize=(10, 5))
plt.plot(time, sap_flux-pld_flux, "k")
plt.xlabel("time [days]")
plt.ylabel("de-trended flux [ppt]")
plt.title("initial de-trended light curve")
plt.xlim(time.min(), time.max());

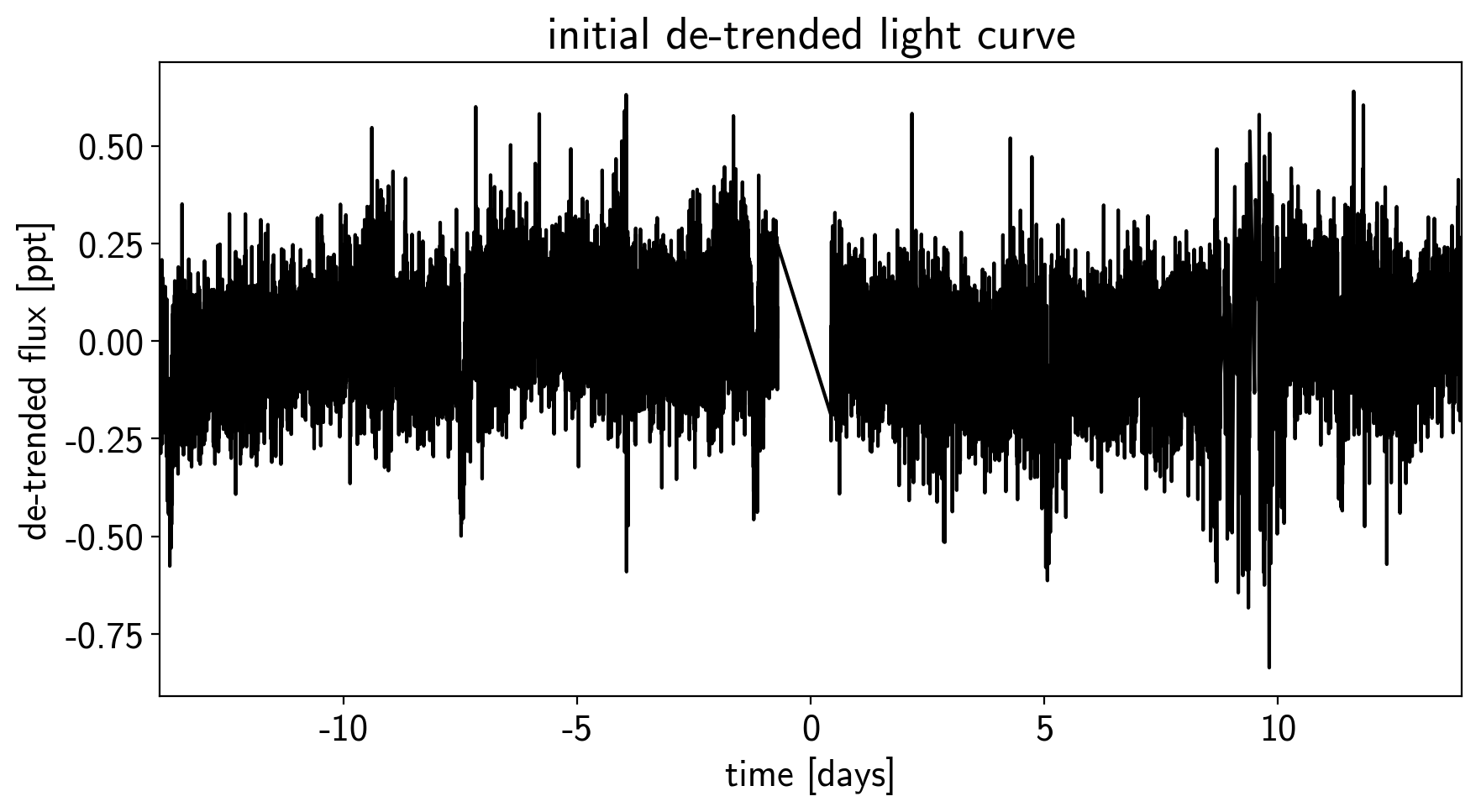
That looks better.

Transit search

Now, let’s use the box least squares periodogram from AstroPy (Note: you’ll need AstroPy v3.1 or more recent to use this feature) to estimate the period, phase, and depth of the transit.

from astropy.stats import BoxLeastSquares

period_grid = np.exp(np.linspace(np.log(1), np.log(15), 50000))

bls = BoxLeastSquares(time, sap_flux - pld_flux)
bls_power = bls.power(period_grid, 0.1, oversample=20)

# Save the highest peak as the planet candidate
index = np.argmax(bls_power.power)
bls_period = bls_power.period[index]
bls_t0 = bls_power.transit_time[index]
bls_depth = bls_power.depth[index]
transit_mask = bls.transit_mask(time, bls_period, 0.2, bls_t0)

fig, axes = plt.subplots(2, 1, figsize=(10, 10))

# Plot the periodogram
ax = axes[0]
ax.axvline(np.log10(bls_period), color="C1", lw=5, alpha=0.8)
ax.plot(np.log10(bls_power.period), bls_power.power, "k")
ax.annotate("period = {0:.4f} d".format(bls_period),
            (0, 1), xycoords="axes fraction",
            xytext=(5, -5), textcoords="offset points",
            va="top", ha="left", fontsize=12)
ax.set_ylabel("bls power")
ax.set_yticks([])
ax.set_xlim(np.log10(period_grid.min()), np.log10(period_grid.max()))
ax.set_xlabel("log10(period)")

# Plot the folded transit
ax = axes[1]
x_fold = (time - bls_t0 + 0.5*bls_period)%bls_period - 0.5*bls_period
m = np.abs(x_fold) < 0.4
ax.plot(x_fold[m], sap_flux[m] - pld_flux[m], ".k")

# Overplot the phase binned light curve
bins = np.linspace(-0.41, 0.41, 32)
denom, _ = np.histogram(x_fold, bins)
num, _ = np.histogram(x_fold, bins, weights=sap_flux - pld_flux)
denom[num == 0] = 1.0
ax.plot(0.5*(bins[1:] + bins[:-1]), num / denom, color="C1")

ax.set_xlim(-0.3, 0.3)
ax.set_ylabel("de-trended flux [ppt]")
ax.set_xlabel("time since transit");

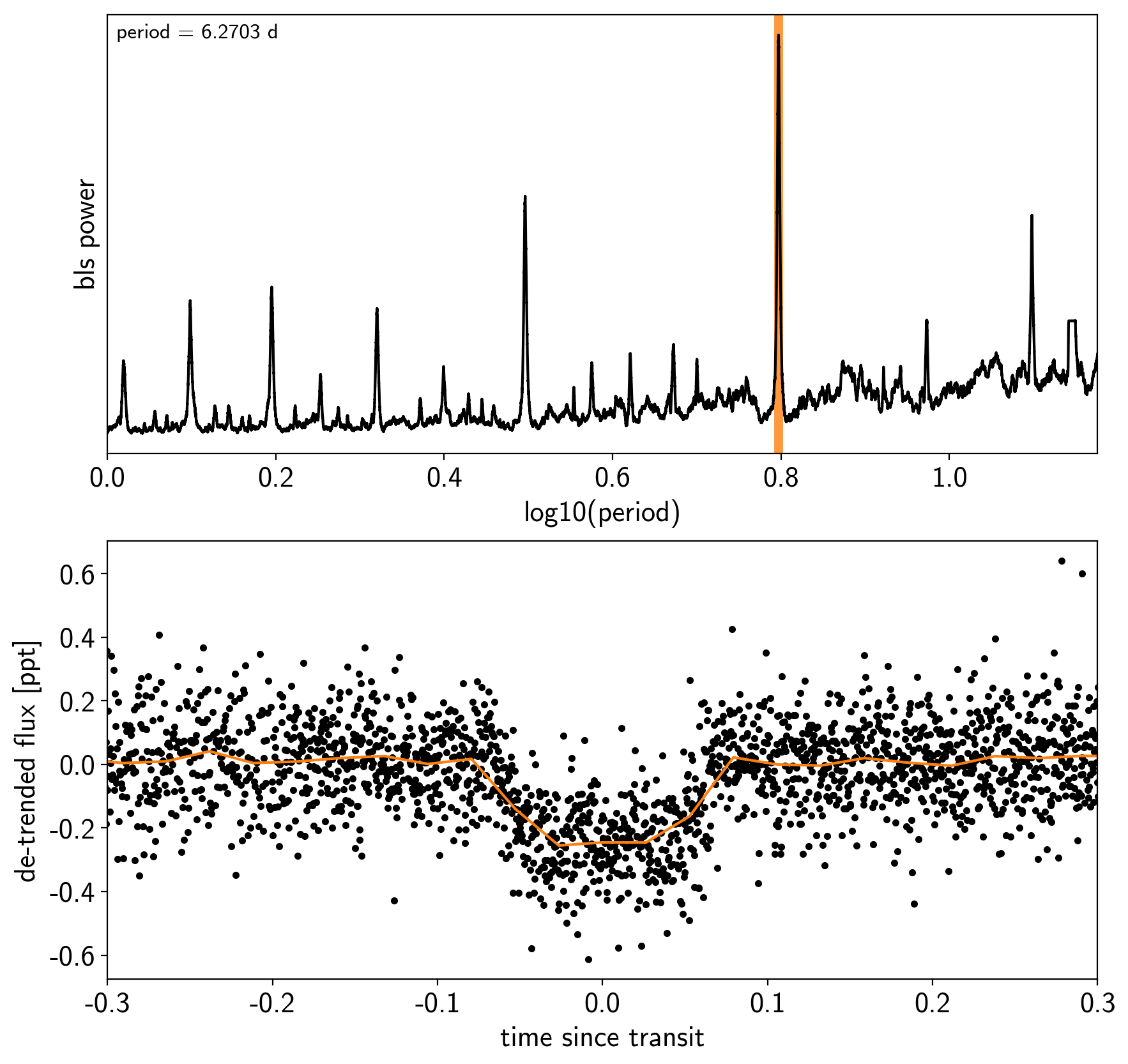
Now that we know where the transits are, it’s generally good practice to de-trend the data one more time with the transits masked so that the de-trending doesn’t overfit the transits. Let’s do that.

m = ~transit_mask
XTX = np.dot(X_pld[m].T, X_pld[m])
w_pld = np.linalg.solve(XTX, np.dot(X_pld[m].T, sap_flux[m]))
pld_flux = np.dot(X_pld, w_pld)

x = np.ascontiguousarray(time, dtype=np.float64)
y = np.ascontiguousarray(sap_flux-pld_flux, dtype=np.float64)

plt.figure(figsize=(10, 5))
plt.plot(time, y, "k")
plt.xlabel("time [days]")
plt.ylabel("de-trended flux [ppt]")
plt.title("final de-trended light curve")
plt.xlim(time.min(), time.max());

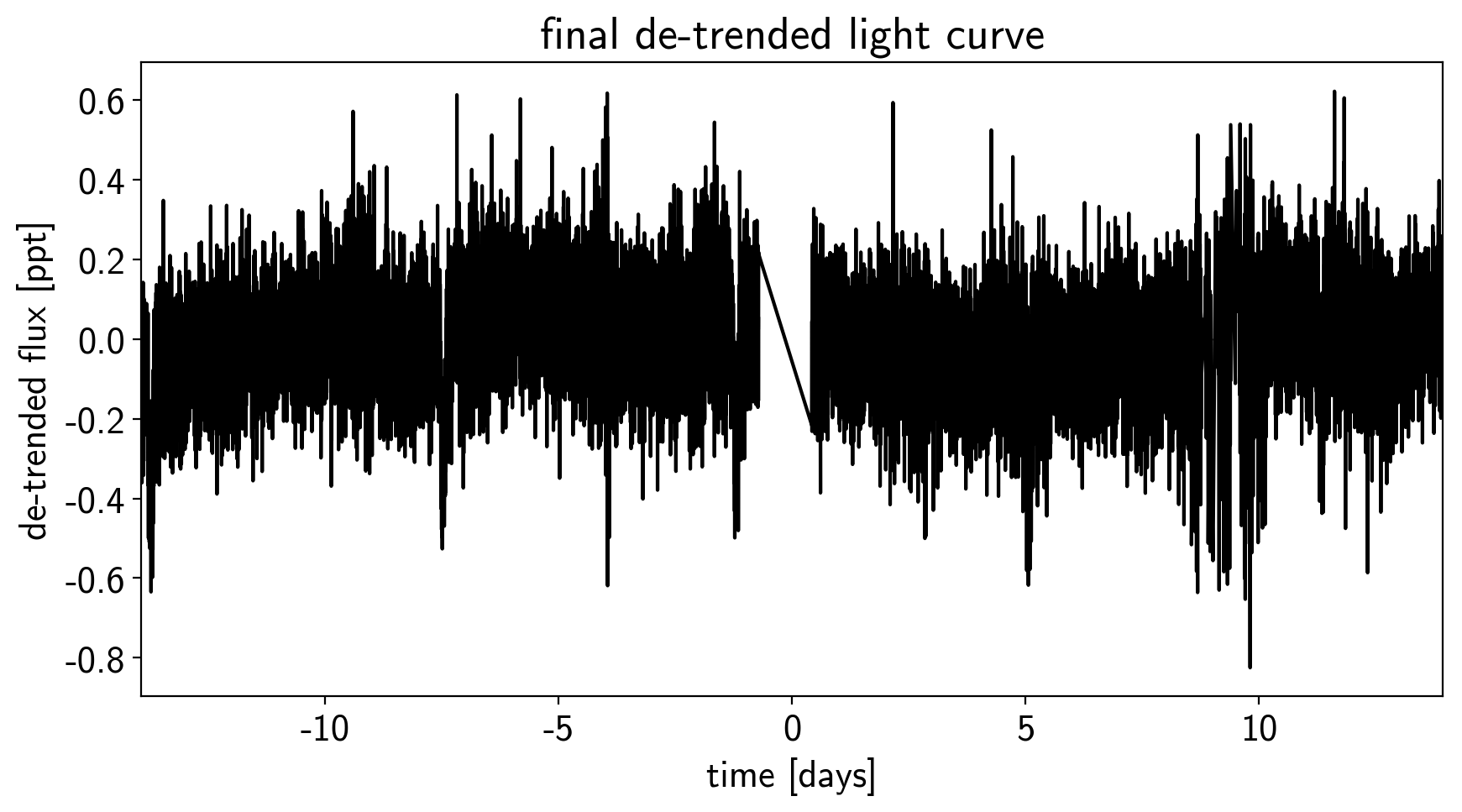
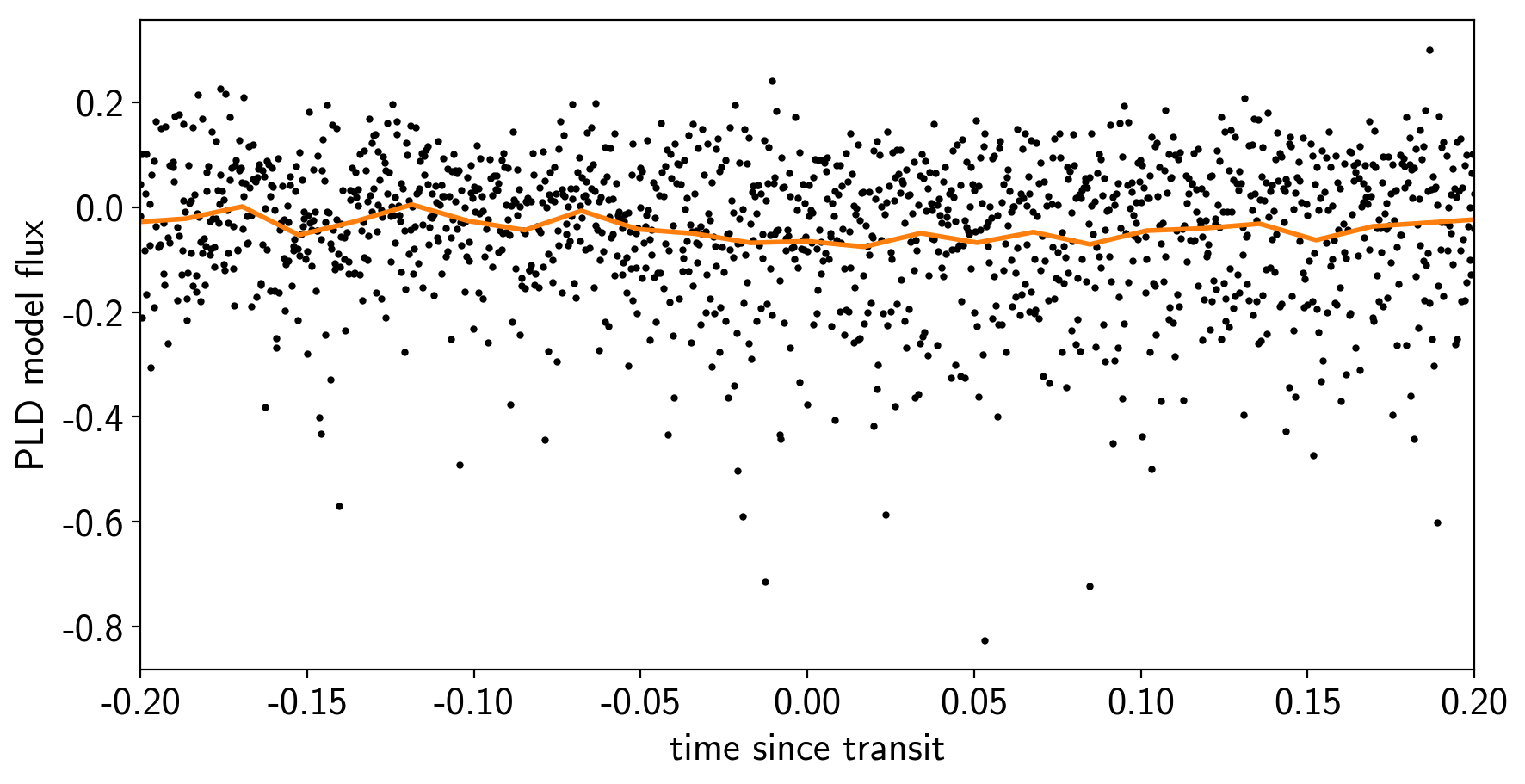
To confirm that we didn’t overfit the transit, we can look at the folded light curve for the PLD model near trasit. This shouldn’t have any residual transit signal, and that looks correct here:

plt.figure(figsize=(10, 5))

x_fold = (x - bls_t0 + 0.5*bls_period) % bls_period - 0.5*bls_period
m = np.abs(x_fold) < 0.3
plt.plot(x_fold[m], pld_flux[m], ".k", ms=4)

bins = np.linspace(-0.5, 0.5, 60)
denom, _ = np.histogram(x_fold, bins)
num, _ = np.histogram(x_fold, bins, weights=pld_flux)
denom[num == 0] = 1.0
plt.plot(0.5*(bins[1:] + bins[:-1]), num / denom, color="C1", lw=2)
plt.xlim(-0.2, 0.2)
plt.xlabel("time since transit")
plt.ylabel("PLD model flux");

The transit model in PyMC3

The transit model, initialization, and sampling are all nearly the same as the one in Case study: K2-24, putting it all together, but we’ll use a more informative prior on eccentricity.

import exoplanet as xo
import pymc3 as pm
import theano.tensor as tt

def build_model(mask=None, start=None):
    if mask is None:
        mask = np.ones(len(x), dtype=bool)
    with pm.Model() as model:

        # Parameters for the stellar properties
        mean = pm.Normal("mean", mu=0.0, sd=10.0)
        u_star = xo.distributions.QuadLimbDark("u_star")

        # Stellar parameters from Huang et al (2018)
        M_star_huang = 1.094, 0.039
        R_star_huang = 1.10, 0.023
        m_star = pm.Normal("m_star", mu=M_star_huang[0], sd=M_star_huang[1])
        r_star = pm.Normal("r_star", mu=R_star_huang[0], sd=R_star_huang[1])

        # Prior to require physical parameters
        pm.Potential("m_star_prior", tt.switch(m_star > 0, 0, -np.inf))
        pm.Potential("r_star_prior", tt.switch(r_star > 0, 0, -np.inf))

        # Orbital parameters for the planets
        logP = pm.Normal("logP", mu=np.log(bls_period), sd=1)
        t0 = pm.Normal("t0", mu=bls_t0, sd=1)
        ror, b = xo.distributions.get_joint_radius_impact(
            min_radius=0.01, max_radius=0.1,
            testval_r=np.sqrt(1e-3)*np.sqrt(bls_depth),
            testval_b=0.5)

        # This is the eccentricity prior from Kipping (2013):
        # https://arxiv.org/abs/1306.4982
        ecc = pm.Beta("ecc", alpha=0.867, beta=3.03, testval=0.1)
        omega = xo.distributions.Angle("omega")

        # Log-uniform prior on ror
        pm.Potential("ror_prior", -tt.log(ror))

        # Transit jitter & GP parameters
        logs2 = pm.Normal("logs2", mu=np.log(np.var(y[mask])), sd=10)
        logS0 = pm.Normal("logS0", mu=np.log(np.var(y[mask])), sd=10)
        logw0 = pm.Normal("logw0", mu=np.log(2*np.pi/10), sd=10)

        # Tracking planet parameters
        period = pm.Deterministic("period", tt.exp(logP))
        r_pl = pm.Deterministic("r_pl", r_star * ror)

        # Orbit model
        orbit = xo.orbits.KeplerianOrbit(
            r_star=r_star, m_star=m_star,
            period=period, t0=t0, b=b,
            ecc=ecc, omega=omega)

        # Compute the model light curve using starry
        light_curves = xo.StarryLightCurve(u_star).get_light_curve(
            orbit=orbit, r=r_pl, t=x[mask], texp=texp)*1e3
        light_curve = pm.math.sum(light_curves, axis=-1) + mean
        pm.Deterministic("light_curves", light_curves)

        # GP model for the light curve
        kernel = xo.gp.terms.SHOTerm(log_S0=logS0, log_w0=logw0, Q=1/np.sqrt(2))
        gp = xo.gp.GP(kernel, x[mask], tt.exp(logs2) + tt.zeros(mask.sum()), J=2)
        pm.Potential("transit_obs", gp.log_likelihood(y[mask] - light_curve))
        pm.Deterministic("gp_pred", gp.predict())

        # Fit for the maximum a posteriori parameters, I've found that I can get
        # a better solution by trying different combinations of parameters in turn
        if start is None:
            start = model.test_point
        map_soln = pm.find_MAP(start=start, vars=[logs2, logS0, logw0])
        map_soln = pm.find_MAP(start=map_soln, vars=[model.rb])
        map_soln = pm.find_MAP(start=map_soln)

    return model, map_soln

model0, map_soln0 = build_model()

logp = 12,994, ||grad|| = 315.08: 100%|██████████| 29/29 [00:00<00:00, 85.92it/s]
logp = 13,001, ||grad|| = 47.911: 100%|██████████| 10/10 [00:00<00:00, 94.58it/s]
logp = 13,020, ||grad|| = 258.8: 100%|██████████| 14/14 [00:00<00:00, 83.02it/s]

Here’s how we plot the initial light curve model:

def plot_light_curve(soln, mask=None):
    if mask is None:
        mask = np.ones(len(x), dtype=bool)

    fig, axes = plt.subplots(3, 1, figsize=(10, 7), sharex=True)

    ax = axes[0]
    ax.plot(x[mask], y[mask], "k", label="data")
    gp_mod = soln["gp_pred"] + soln["mean"]
    ax.plot(x[mask], gp_mod, color="C2", label="gp model")
    ax.legend(fontsize=10)
    ax.set_ylabel("relative flux [ppt]")

    ax = axes[1]
    ax.plot(x[mask], y[mask] - gp_mod, "k", label="de-trended data")
    for i, l in enumerate("b"):
        mod = soln["light_curves"][:, i]
        ax.plot(x[mask], mod, label="planet {0}".format(l))
    ax.legend(fontsize=10, loc=3)
    ax.set_ylabel("de-trended flux [ppt]")

    ax = axes[2]
    mod = gp_mod + np.sum(soln["light_curves"], axis=-1)
    ax.plot(x[mask], y[mask] - mod, "k")
    ax.axhline(0, color="#aaaaaa", lw=1)
    ax.set_ylabel("residuals [ppt]")
    ax.set_xlim(x[mask].min(), x[mask].max())
    ax.set_xlabel("time [days]")

    return fig

plot_light_curve(map_soln0);

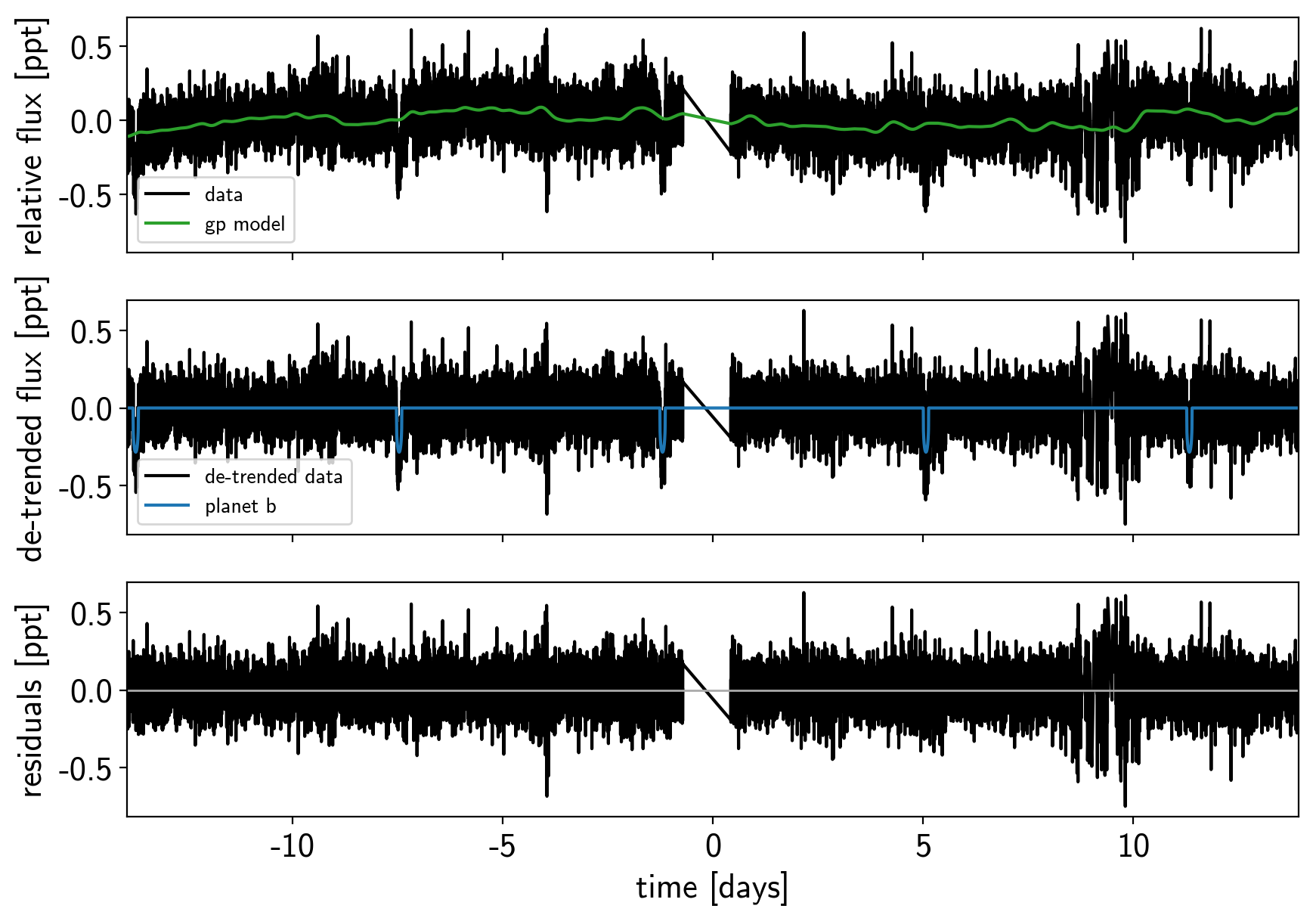
As in the Case study: K2-24, putting it all together tutorial, we can do some sigma clipping to remove significant outliers.

mod = map_soln0["gp_pred"] + map_soln0["mean"] + np.sum(map_soln0["light_curves"], axis=-1)
resid = y - mod
rms = np.sqrt(np.median(resid**2))
mask = np.abs(resid) < 5 * rms

plt.figure(figsize=(10, 5))
plt.plot(x, resid, "k", label="data")
plt.plot(x[~mask], resid[~mask], "xr", label="outliers")
plt.axhline(0, color="#aaaaaa", lw=1)
plt.ylabel("residuals [ppt]")
plt.xlabel("time [days]")
plt.legend(fontsize=12, loc=3)
plt.xlim(x.min(), x.max());

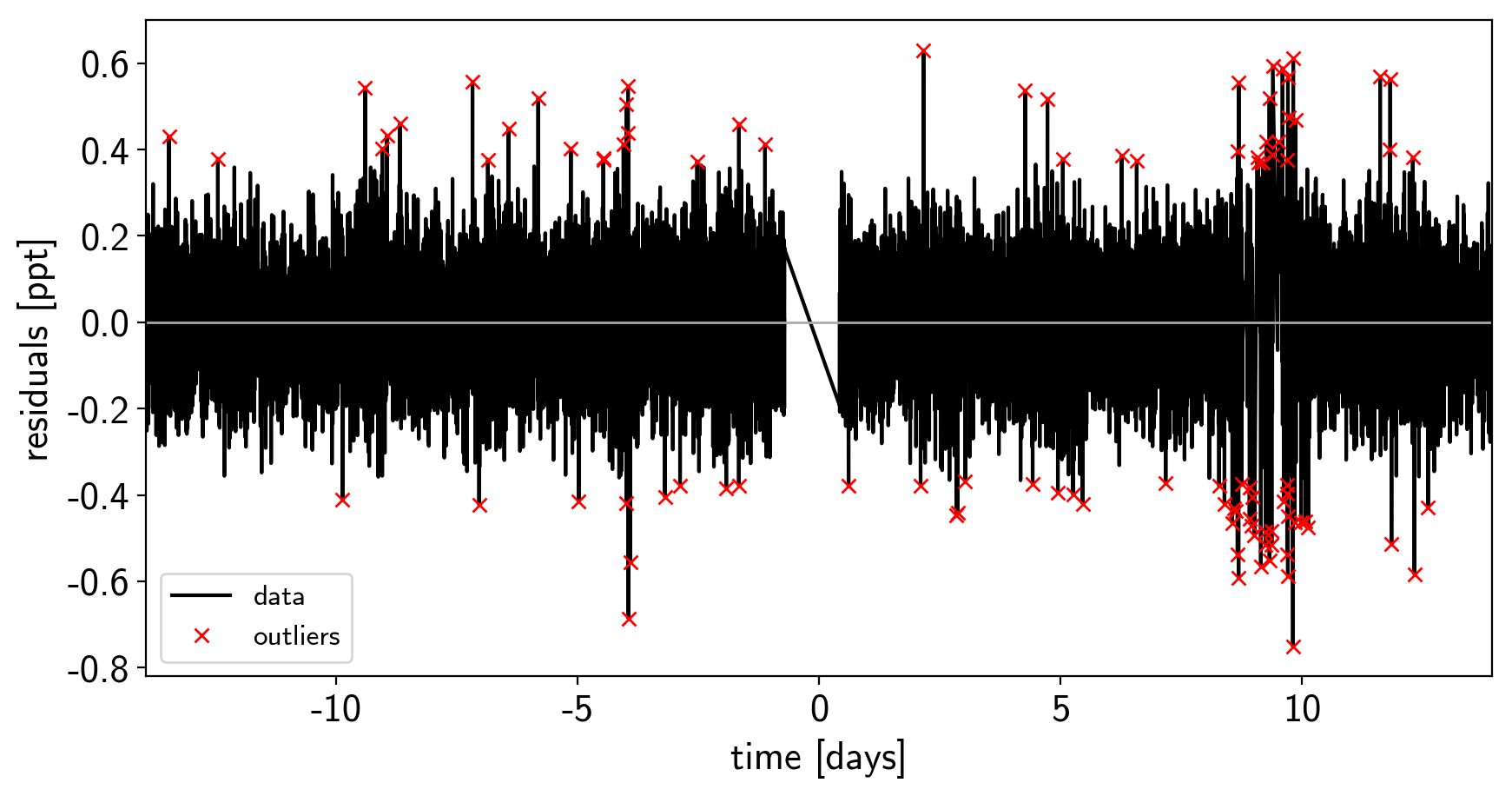
And then we re-build the model using the data without outliers.

model, map_soln = build_model(mask, map_soln0)
plot_light_curve(map_soln, mask);

logp = 13,724, ||grad|| = 1.7255: 100%|██████████| 17/17 [00:00<00:00, 89.34it/s]
logp = 13,724, ||grad|| = 11.222: 100%|██████████| 8/8 [00:00<00:00, 109.98it/s]
logp = 13,724, ||grad|| = 48.236: 100%|██████████| 12/12 [00:00<00:00, 85.13it/s]

Now that we have the model, we can sample it using a exoplanet.PyMC3Sampler:

np.random.seed(42)
sampler = xo.PyMC3Sampler(window=100, start=200, finish=200)
with model:
    burnin = sampler.tune(tune=3000, start=map_soln, step_kwargs=dict(target_accept=0.9))

Sampling 4 chains: 100%|██████████| 808/808 [06:51<00:00,  3.23s/draws]
Sampling 4 chains: 100%|██████████| 408/408 [03:22<00:00,  2.02s/draws]
Sampling 4 chains: 100%|██████████| 808/808 [06:32<00:00,  1.80s/draws]
Sampling 4 chains: 100%|██████████| 1608/1608 [15:13<00:00,  1.55s/draws]
Sampling 4 chains: 100%|██████████| 8408/8408 [1:13:25<00:00,  2.17s/draws]

with model:
    trace = sampler.sample(draws=2000)

Multiprocess sampling (4 chains in 4 jobs)
NUTS: [logw0, logS0, logs2, omega, ecc, rb, t0, logP, r_star, m_star, u_star, mean]
Sampling 4 chains: 100%|██████████| 8800/8800 [1:55:09<00:00,  3.46s/draws]
There were 3 divergences after tuning. Increase target_accept or reparameterize.
There were 46 divergences after tuning. Increase target_accept or reparameterize.
There were 11 divergences after tuning. Increase target_accept or reparameterize.
There were 17 divergences after tuning. Increase target_accept or reparameterize.
The number of effective samples is smaller than 25% for some parameters.

pm.summary(trace, varnames=["logw0", "logS0", "logs2", "omega", "ecc", "r", "b", "t0", "logP", "r_star", "m_star", "u_star", "mean"])

	mean	sd	mc_error	hpd_2.5	hpd_97.5	n_eff	Rhat
logw0	1.169933	0.134382	1.710553e-03	9.057975e-01	1.426173	5380.444081	1.000417
logS0	-6.794914	0.340207	4.232829e-03	-7.430404e+00	-6.112015	5193.502252	0.999900
logs2	-4.383342	0.010547	1.218625e-04	-4.403523e+00	-4.362676	6670.767506	0.999829
omega	0.741572	1.685123	3.409555e-02	-2.847012e+00	3.139181	2228.642932	1.000115
ecc	0.199290	0.143478	2.788730e-03	7.505986e-07	0.483658	2205.279438	1.001101
r__0	0.015617	0.000447	1.265344e-05	1.481963e-02	0.016442	1136.195700	1.001984
b__0	0.407585	0.192050	4.839018e-03	3.120207e-02	0.649304	1444.097405	1.000071
t0	-1.197506	0.000668	1.236398e-05	-1.198828e+00	-1.196184	2557.054774	1.000829
logP	1.835392	0.000075	9.508086e-07	1.835247e+00	1.835527	5164.781290	0.999993
r_star	1.098558	0.023103	2.872805e-04	1.054516e+00	1.144394	6021.620225	1.000639
m_star	1.095636	0.038200	4.404067e-04	1.022309e+00	1.170718	7402.759081	0.999830
u_star__0	0.195088	0.163378	2.450729e-03	1.297818e-04	0.523474	4238.611904	1.000690
u_star__1	0.523479	0.263035	4.398927e-03	-1.104263e-02	0.955436	3107.721682	1.000902
mean	-0.001184	0.009222	1.212084e-04	-1.939158e-02	0.016804	6015.058717	1.000076

Results

After sampling, we can make the usual plots. First, let’s look at the folded light curve plot:

# Compute the GP prediction
gp_mod = np.median(trace["gp_pred"] + trace["mean"][:, None], axis=0)

# Get the posterior median orbital parameters
p = np.median(trace["period"])
t0 = np.median(trace["t0"])

# Plot the folded data
x_fold = (x[mask] - t0 + 0.5*p) % p - 0.5*p
plt.plot(x_fold, y[mask] - gp_mod, ".k", label="data", zorder=-1000)

# Overplot the phase binned light curve
bins = np.linspace(-0.41, 0.41, 50)
denom, _ = np.histogram(x_fold, bins)
num, _ = np.histogram(x_fold, bins, weights=y[mask])
denom[num == 0] = 1.0
plt.plot(0.5*(bins[1:] + bins[:-1]), num / denom, "o", color="C2",
         label="binned")

# Plot the folded model
inds = np.argsort(x_fold)
inds = inds[np.abs(x_fold)[inds] < 0.3]
pred = trace["light_curves"][:, inds, 0]
pred = np.percentile(pred, [16, 50, 84], axis=0)
plt.plot(x_fold[inds], pred[1], color="C1", label="model")
art = plt.fill_between(x_fold[inds], pred[0], pred[2], color="C1", alpha=0.5,
                       zorder=1000)
art.set_edgecolor("none")

# Annotate the plot with the planet's period
txt = "period = {0:.5f} +/- {1:.5f} d".format(
    np.mean(trace["period"]), np.std(trace["period"]))
plt.annotate(txt, (0, 0), xycoords="axes fraction",
             xytext=(5, 5), textcoords="offset points",
             ha="left", va="bottom", fontsize=12)

plt.legend(fontsize=10, loc=4)
plt.xlim(-0.5*p, 0.5*p)
plt.xlabel("time since transit [days]")
plt.ylabel("de-trended flux")
plt.xlim(-0.15, 0.15);

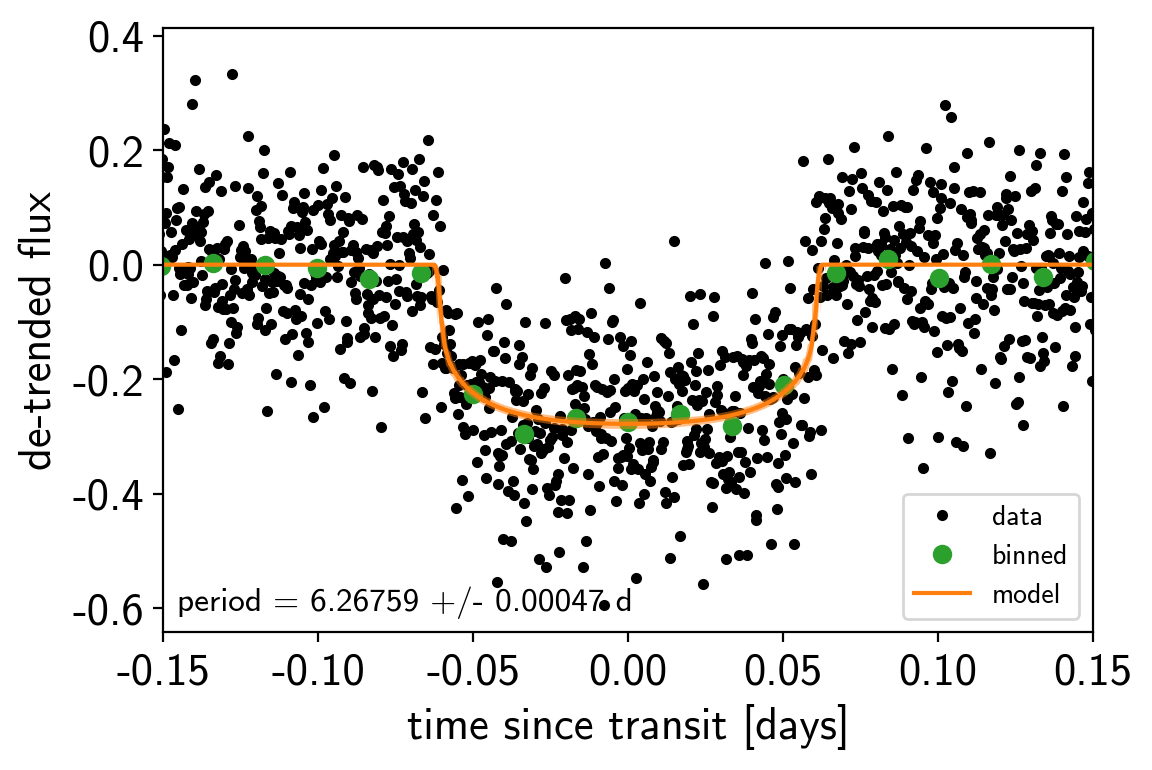
And a corner plot of some of the key parameters:

import corner
import astropy.units as u
varnames = ["period", "b", "ecc", "r_pl"]
samples = pm.trace_to_dataframe(trace, varnames=varnames)

# Convert the radius to Earth radii
samples["r_pl"] = (np.array(samples["r_pl__0"]) * u.R_sun).to(u.R_earth).value
del samples["r_pl__0"]

corner.corner(
    samples[["period", "r_pl", "b__0", "ecc"]],
    labels=["period [days]", "radius [Earth radii]", "impact param", "eccentricity"]);

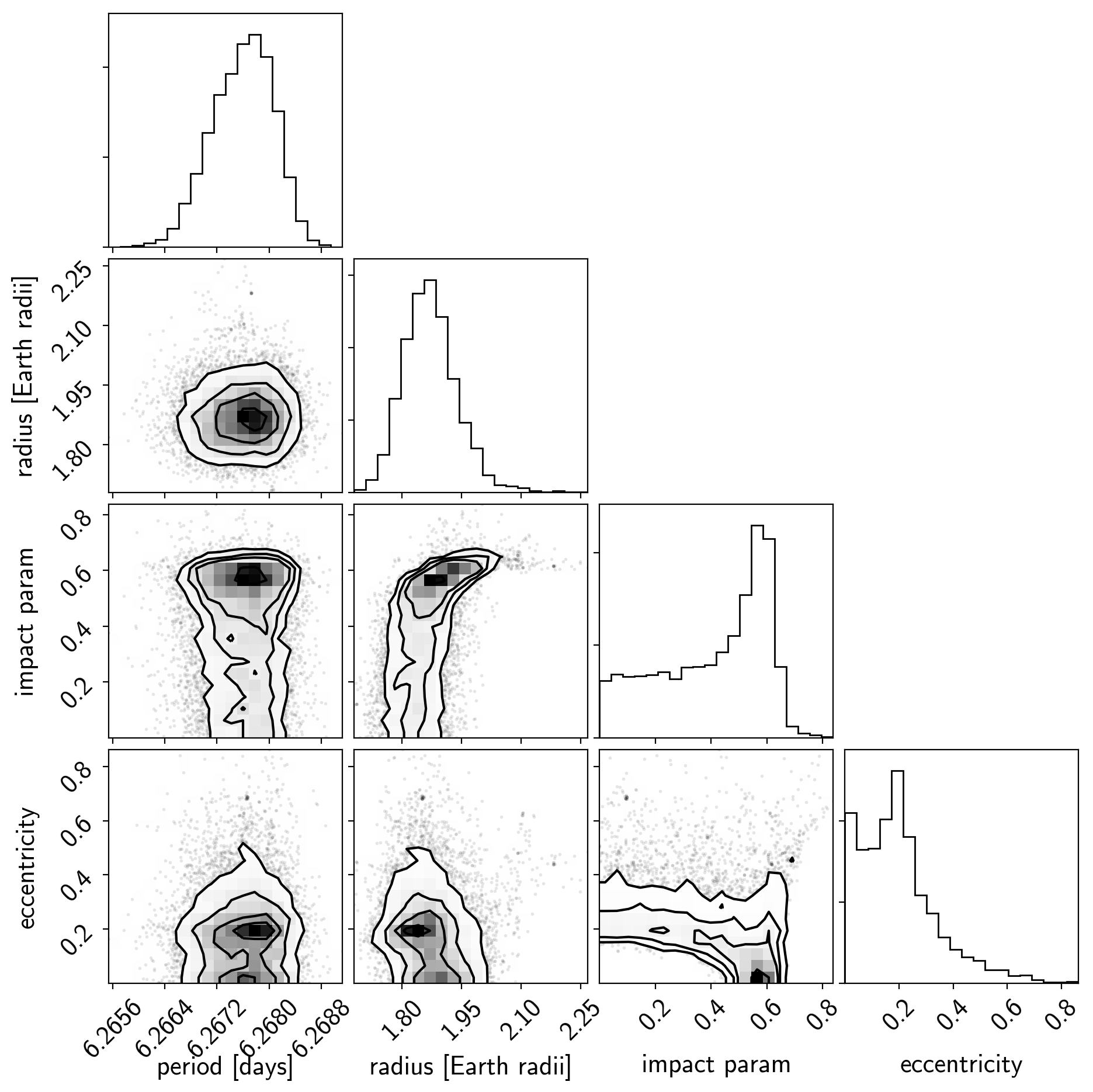
These all seem consistent with the previously published values and an earlier inconsistency between this radius measurement and the literature has been resolved by fixing a bug in exoplanet.