Note
This tutorial was generated from an IPython notebook that can be downloaded here.
theano version: 1.0.3
pymc3 version: 3.5
exoplanet version: 0.1.4
Gaussian process models for stellar variability¶
When fitting exoplanets, we also need to fit for the stellar variability and Gaussian Processes (GPs) are often a good descriptive model for this variation. PyMC3 has support for all sorts of general GP models, but exoplanet includes support for scalable 1D GPs (see gp for more info) that can work with large datasets. In this tutorial, we go through the process of modeling the light curve of a rotating star observed by Kepler using exoplanet.
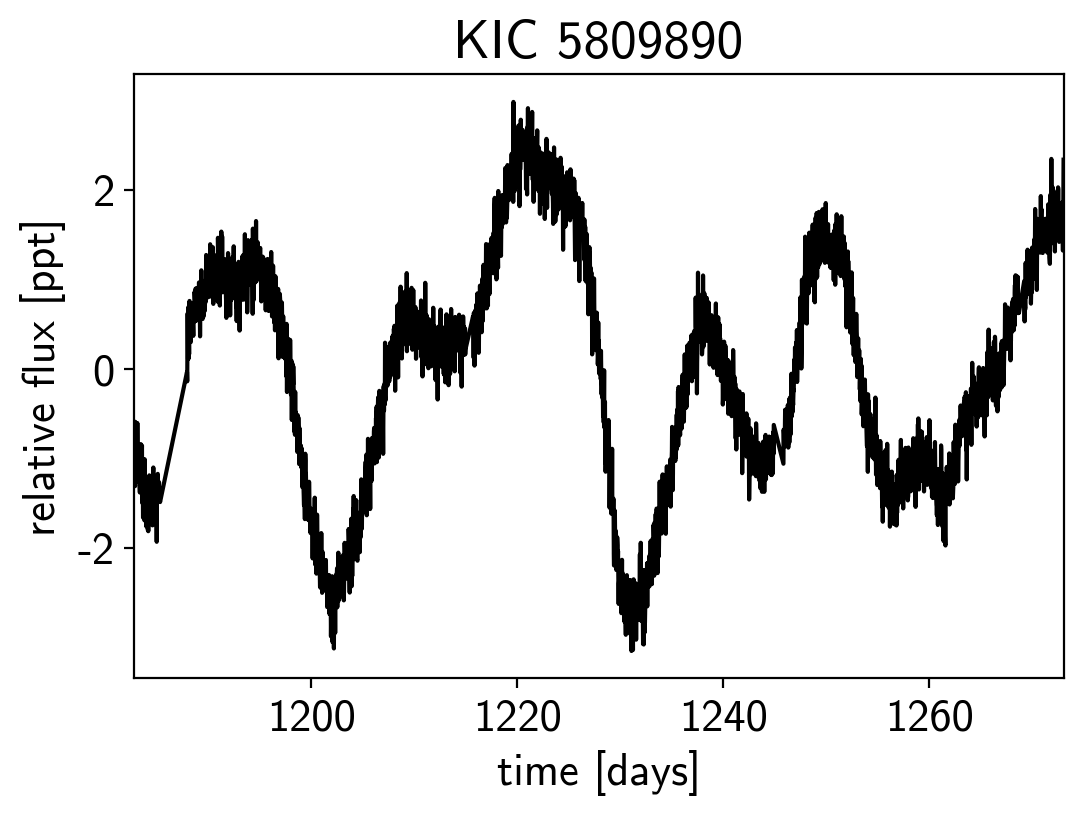
First, let’s download and plot the data:
import numpy as np
import matplotlib.pyplot as plt
from astropy.io import fits
url = "https://archive.stsci.edu/missions/kepler/lightcurves/0058/005809890/kplr005809890-2012179063303_llc.fits"
with fits.open(url) as hdus:
data = hdus[1].data
x = data["TIME"]
y = data["PDCSAP_FLUX"]
yerr = data["PDCSAP_FLUX_ERR"]
m = (data["SAP_QUALITY"] == 0) & np.isfinite(x) & np.isfinite(y)
x = np.ascontiguousarray(x[m], dtype=np.float64)
y = np.ascontiguousarray(y[m], dtype=np.float64)
yerr = np.ascontiguousarray(yerr[m], dtype=np.float64)
mu = np.mean(y)
y = (y / mu - 1) * 1e3
yerr = yerr * 1e3 / mu
plt.plot(x, y, "k")
plt.xlim(x.min(), x.max())
plt.xlabel("time [days]")
plt.ylabel("relative flux [ppt]")
plt.title("KIC 5809890");
A Gaussian process model for stellar variability¶
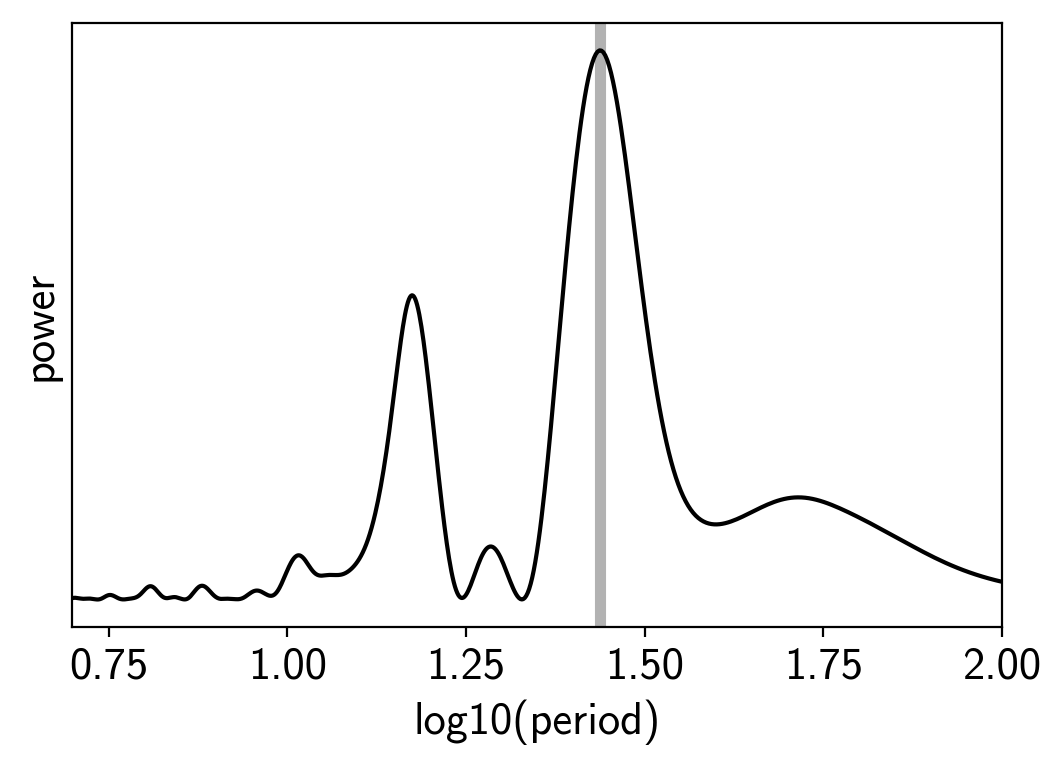
This looks like the light curve of a rotating star, and it has been shown that it is possible to model this variability by using a quasiperiodic Gaussian process. To start with, let’s get an estimate of the rotation period using the Lomb-Scargle periodogram:
import exoplanet as xo
results = xo.estimators.lomb_scargle_estimator(
x, y, max_peaks=1, min_period=5.0, max_period=100.0,
samples_per_peak=50)
peak = results["peaks"][0]
freq, power = results["periodogram"]
plt.plot(-np.log10(freq), power, "k")
plt.axvline(np.log10(peak["period"]), color="k", lw=4, alpha=0.3)
plt.xlim((-np.log10(freq)).min(), (-np.log10(freq)).max())
plt.yticks([])
plt.xlabel("log10(period)")
plt.ylabel("power");
Now, using this initialization, we can set up the GP model in
exoplanet. We’ll use the exoplanet.gp.terms.RotationTerm
kernel that is a mixture of two simple harmonic oscillators with periods
separated by a factor of two. As you can see from the periodogram above,
this might be a good model for this light curve and I’ve found that it
works well in many cases.
import pymc3 as pm
import theano.tensor as tt
with pm.Model() as model:
# The mean flux of the time series
mean = pm.Normal("mean", mu=0.0, sd=10.0)
# A jitter term describing excess white noise
logs2 = pm.Normal("logs2", mu=2*np.log(np.min(yerr)), sd=5.0)
# The parameters of the RotationTerm kernel
logamp = pm.Normal("logamp", mu=np.log(np.var(y)), sd=5.0)
logperiod = pm.Normal("logperiod", mu=np.log(peak["period"]), sd=5.0)
logQ0 = pm.Normal("logQ0", mu=1.0, sd=10.0)
logdeltaQ = pm.Normal("logdeltaQ", mu=2.0, sd=10.0)
mix = pm.Uniform("mix", lower=0, upper=1.0)
# Track the period as a deterministic
period = pm.Deterministic("period", tt.exp(logperiod))
# Set up the Gaussian Process model
kernel = xo.gp.terms.RotationTerm(
log_amp=logamp,
period=period,
log_Q0=logQ0,
log_deltaQ=logdeltaQ,
mix=mix
)
gp = xo.gp.GP(kernel, x, yerr**2 + tt.exp(logs2), J=4)
# Compute the Gaussian Process likelihood and add it into the
# the PyMC3 model as a "potential"
pm.Potential("loglike", gp.log_likelihood(y - mean))
# Compute the mean model prediction for plotting purposes
pm.Deterministic("pred", gp.predict())
# Optimize to find the maximum a posteriori parameters
map_soln = xo.optimize(start=model.test_point)
success: True
initial logp: 515.8061433751361
final logp: 692.7159093513108
Now that we have the model set up, let’s plot the maximum a posteriori model prediction.
plt.plot(x, y, "k", label="data")
plt.plot(x, map_soln["pred"], color="C1", label="model")
plt.xlim(x.min(), x.max())
plt.legend(fontsize=10)
plt.xlabel("time [days]")
plt.ylabel("relative flux [ppt]")
plt.title("KIC 5809890; map model");
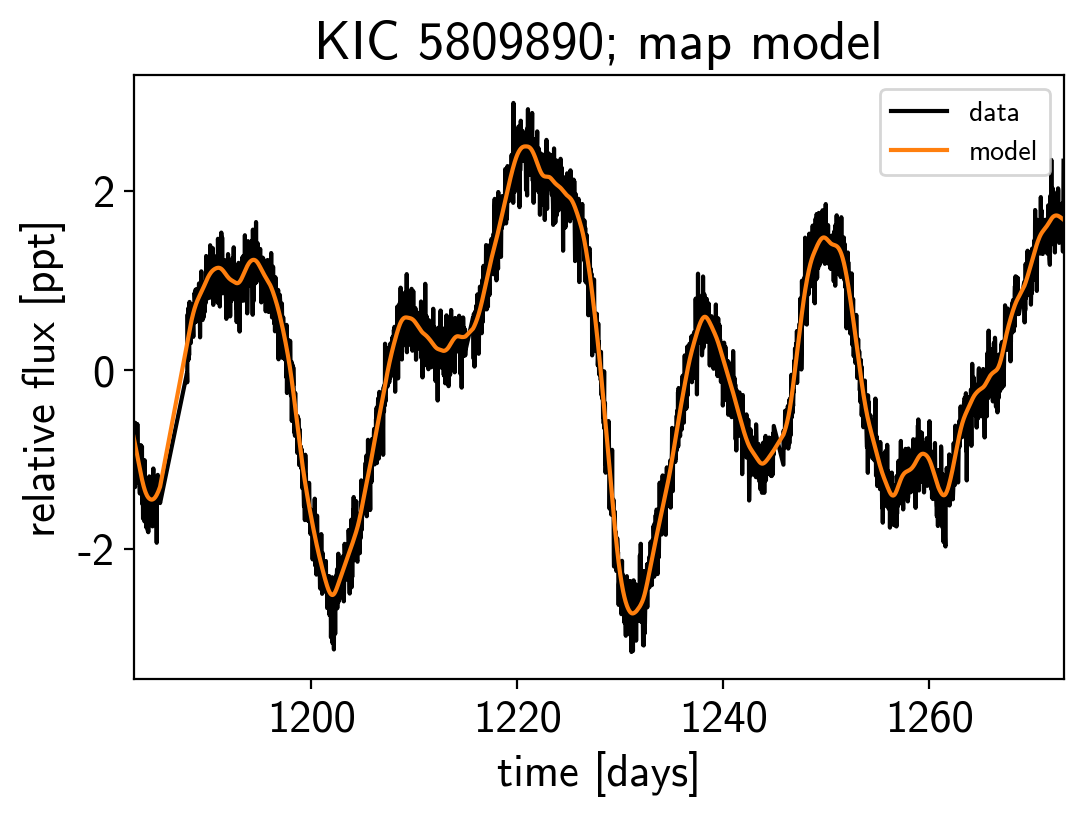
That looks pretty good! Now let’s sample from the posterior using a
exoplanet.PyMC3Sampler.
np.random.seed(42)
sampler = xo.PyMC3Sampler(finish=200)
with model:
sampler.tune(tune=2000, start=map_soln, step_kwargs=dict(target_accept=0.9))
trace = sampler.sample(draws=2000)
Sampling 2 chains: 100%|██████████| 154/154 [00:25<00:00, 5.46draws/s] Sampling 2 chains: 100%|██████████| 54/54 [00:07<00:00, 7.54draws/s] Sampling 2 chains: 100%|██████████| 104/104 [00:02<00:00, 39.41draws/s] Sampling 2 chains: 100%|██████████| 204/204 [00:07<00:00, 29.66draws/s] Sampling 2 chains: 100%|██████████| 404/404 [00:14<00:00, 10.64draws/s] Sampling 2 chains: 100%|██████████| 804/804 [00:25<00:00, 31.46draws/s] Sampling 2 chains: 100%|██████████| 2304/2304 [02:14<00:00, 9.03draws/s] Sampling 2 chains: 100%|██████████| 404/404 [00:15<00:00, 18.00draws/s] Multiprocess sampling (2 chains in 2 jobs) NUTS: [mix, logdeltaQ, logQ0, logperiod, logamp, logs2, mean] Sampling 2 chains: 100%|██████████| 4000/4000 [02:08<00:00, 31.18draws/s] There were 2 divergences after tuning. Increase target_accept or reparameterize.
Now we can do the usual convergence checks:
pm.summary(trace, varnames=["mix", "logdeltaQ", "logQ0", "logperiod", "logamp", "logs2", "mean"])
| mean | sd | mc_error | hpd_2.5 | hpd_97.5 | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|
| mix | 0.635327 | 0.246691 | 0.007100 | 0.194223 | 0.999948 | 1147.772615 | 1.000038 |
| logdeltaQ | 1.892032 | 9.773862 | 0.269028 | -16.527806 | 22.899390 | 1239.739908 | 1.000290 |
| logQ0 | 0.575256 | 0.548974 | 0.013103 | -0.462753 | 1.653936 | 2068.742721 | 1.000698 |
| logperiod | 3.341504 | 0.105432 | 0.003043 | 3.162129 | 3.589702 | 1432.254264 | 0.999874 |
| logamp | 0.412084 | 0.595942 | 0.018519 | -0.554424 | 1.638109 | 1070.612437 | 0.999828 |
| logs2 | -4.965113 | 0.126026 | 0.003008 | -5.204822 | -4.712618 | 2146.926491 | 0.999827 |
| mean | -0.020345 | 0.216496 | 0.005216 | -0.425458 | 0.407064 | 1660.287239 | 0.999773 |
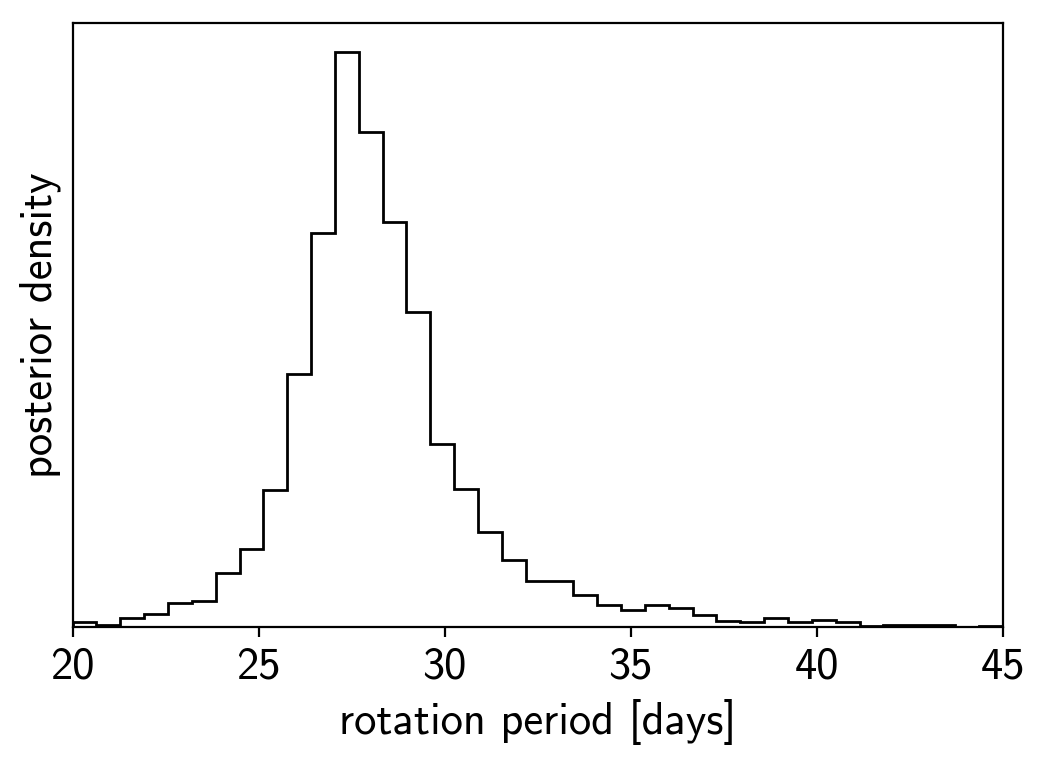
And plot the posterior distribution over rotation period:
period_samples = trace["period"]
bins = np.linspace(20, 45, 40)
plt.hist(period_samples, bins, histtype="step", color="k")
plt.yticks([])
plt.xlim(bins.min(), bins.max())
plt.xlabel("rotation period [days]")
plt.ylabel("posterior density");