A quick intro to PyMC#
import exoplanet
exoplanet.utils.docs_setup()
print(f"exoplanet.__version__ = '{exoplanet.__version__}'")
WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.
exoplanet.__version__ = '0.6.0'
Gradient-based inference methods (like Hamiltonian Monte Carlo (HMC)) haven’t been widely used in astrophysics, but they are the standard methods for probabilistic inference using Markov chain Monte Carlo (MCMC) in many other fields. exoplanet is designed to provide the building blocks for fitting many exoplanet datasets using this technology, and this tutorial presents some of the basic features of the PyMC modeling language and inference engine. The documentation for PyMC includes many other tutorials that you should check out to get more familiar with the features that are available.
In this tutorial, we will go through two simple examples of fitting some data using PyMC. The first is the classic fitting a line to data with unknown error bars, and the second is a more relevant example where we fit a radial velocity model to the public radial velocity observations of 51 Peg. You can read more about fitting lines to data in the bible of line fitting and you can see another example of fitting the 51 Peg data using HMC (this time using Stan) here.
Hello world (AKA fitting a line to data)#
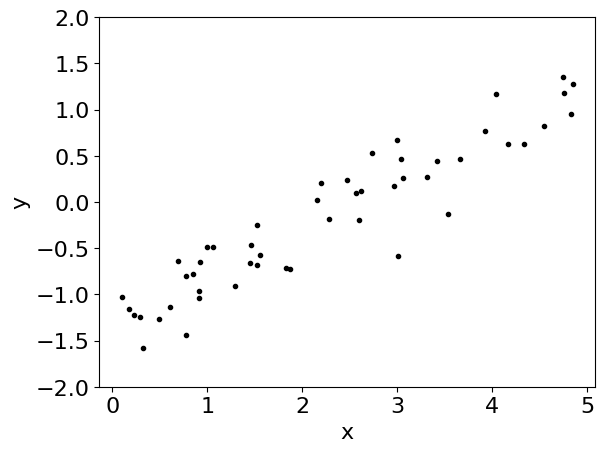
My standard intro to a new modeling language or inference framework is to fit a line to data. So. Let’s do that with PyMC.
To start, we’ll generate some fake data using a linear model. Feel free to change the random number seed to try out a different dataset.
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
true_m = 0.5
true_b = -1.3
true_logs = np.log(0.3)
x = np.sort(np.random.uniform(0, 5, 50))
y = true_b + true_m * x + np.exp(true_logs) * np.random.randn(len(x))
plt.plot(x, y, ".k")
plt.ylim(-2, 2)
plt.xlabel("x")
_ = plt.ylabel("y")
To fit a model to these data, our model will have 3 parameters: the slope \(m\), the intercept \(b\), and the log of the uncertainty \(\log(\sigma)\). To start, let’s choose broad uniform priors on these parameters:
Then, the log-likelihood function will be
[Note: the second normalization term is needed in this model because we are fitting for \(\sigma\) and the second term is not a constant.]
Another way of writing this model that might not be familiar is the following:
This is the way that a model like this is often defined in statistics and it will be useful when we implement out model in PyMC so take a moment to make sure that you understand the notation.
Now, let’s implement this model in PyMC. The documentation for the distributions available in PyMC’s modeling language can be found here and these will come in handy as you go on to write your own models.
import pymc as pm
with pm.Model() as model:
# Define the priors on each parameter:
m = pm.Uniform("m", lower=-5, upper=5)
b = pm.Uniform("b", lower=-5, upper=5)
logs = pm.Uniform("logs", lower=-5, upper=5)
# Define the likelihood. A few comments:
# 1. For mathematical operations like "exp", you can't use
# numpy. Instead, use the mathematical operations defined
# in "pm.math".
# 2. To condition on data, you use the "observed" keyword
# argument to any distribution. In this case, we want to
# use the "Normal" distribution (look up the docs for
# this).
pm.Normal("obs", mu=m * x + b, sigma=pm.math.exp(logs), observed=y)
# This is how you will sample the model. Take a look at the
# docs to see that other parameters that are available.
trace = pm.sample(draws=1000, tune=1000, chains=2, cores=2)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [m, b, logs]
/home/docs/checkouts/readthedocs.org/user_builds/exoplanet/envs/latest/lib/python3.10/site-packages/rich/live.py:23
1: UserWarning: install "ipywidgets" for Jupyter support
warnings.warn('install "ipywidgets" for Jupyter support')
Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 7 seconds.
We recommend running at least 4 chains for robust computation of convergence diagnostics
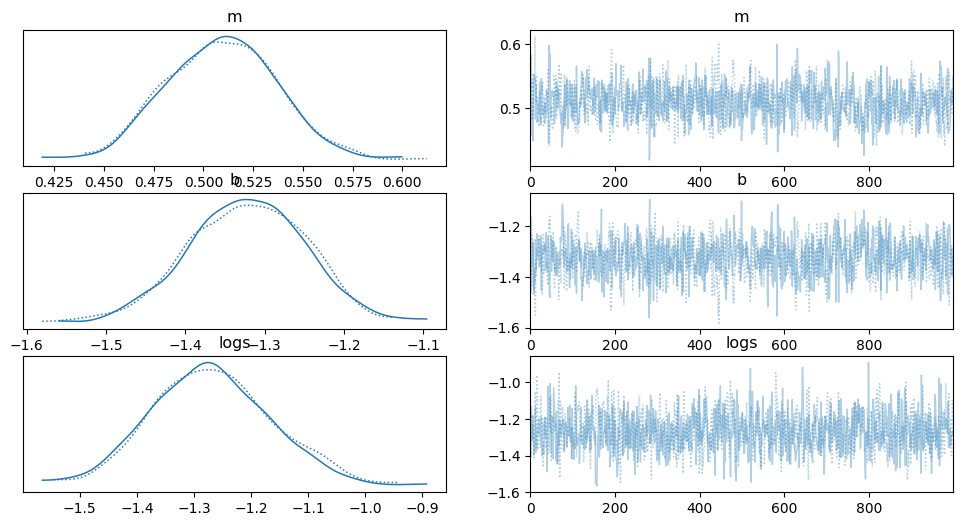
Now since we now have samples, let’s make some diagnostic plots. The first plot to look at is the “traceplot” implemented in PyMC. In this plot, you’ll see the marginalized distribution for each parameter on the left and the trace plot (parameter value as a function of step number) on the right. In each panel, you should see two lines with different colors or linestyles. These are the results of different independent chains and if the results are substantially different in the different chains then there is probably something going wrong.
import arviz as az
_ = az.plot_trace(trace, var_names=["m", "b", "logs"])
It’s also good to quantify that “looking substantially different” argument.
This is implemented in PyMC as the “summary” function.
In this table, some of the key columns to look at are the columns starting with ess_ and Rhat.
The
ess_*columns show an estimate of the number of effective (or independent) samples for that parameter. In this case, theessshould probably be around 500 per chain (there should have been 2 chains run).Rhatshows the Gelman–Rubin statistic, and it should be close to 1.
az.summary(trace, var_names=["m", "b", "logs"])
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| m | 0.509 | 0.027 | 0.458 | 0.557 | 0.001 | 0.001 | 975.0 | 1040.0 | 1.0 |
| b | -1.323 | 0.073 | -1.463 | -1.194 | 0.002 | 0.002 | 983.0 | 1122.0 | 1.0 |
| logs | -1.269 | 0.105 | -1.458 | -1.070 | 0.003 | 0.002 | 1156.0 | 976.0 | 1.0 |
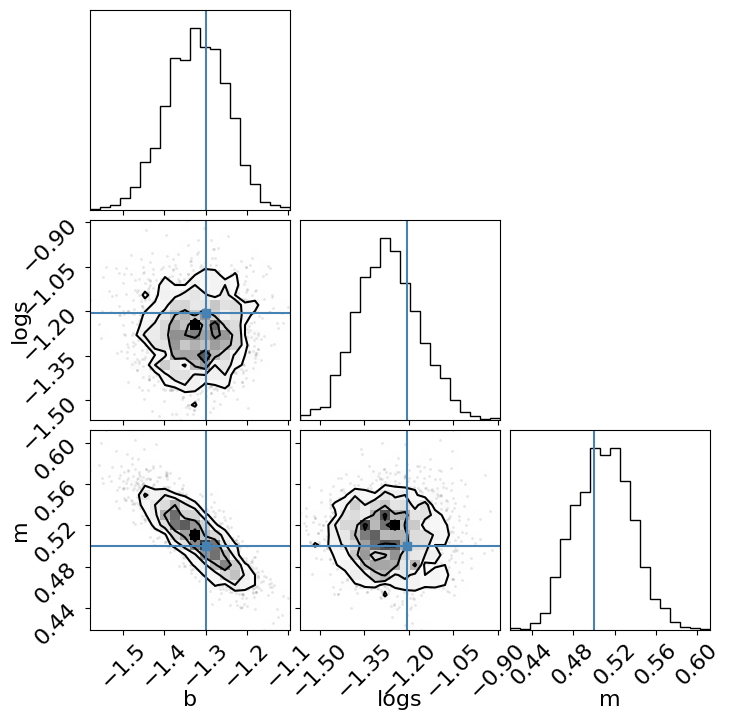
The last diagnostic plot that we’ll make here is the corner plot made using corner.py.
import corner
_ = corner.corner(
trace,
truths=dict(m=true_m, b=true_b, logs=true_logs),
)
Extra credit: Here are a few suggestions for things to try out while getting more familiar with PyMC:
Try initializing the parameters using the
initvalargument to the distributions. Does this improve performance in this case? It will substantially improve performance in more complicated examples.Try changing the priors on the parameters. For example, try the “uninformative” prior recommended by Jake VanderPlas on his blog.
What happens as you substantially increase or decrease the simulated noise? Does the performance change significantly? Why?
A more realistic example: radial velocity exoplanets#
While the above example was cute, it doesn’t really fully exploit the power of PyMC and it doesn’t really show some of the real issues that you will face when you use PyMC as an astronomer. To get a better sense of how you might use PyMC in Real Life™, let’s take a look at a more realistic example: fitting a Keplerian orbit to radial velocity observations.
One of the key aspects of this problem that I want to highlight is the fact that PyMC (and the underlying model-building framework PyTensor) don’t have out-of-the-box support for the root-finding that is required to solve Kepler’s equation. As part of the process of computing a Keplerian RV model, we must solve the equation:
for the eccentric anomaly \(E\) given some mean anomaly \(M\) and eccentricity \(e\). There are commonly accepted methods of solving this equation using Newton’s method, but if we want to expose that to PyMC, we have to define a custom Pytensor operation with a custom gradient. I won’t go into the details of the math (because I blogged about it) and I won’t go into the details of the implementation. So, for this tutorial, we’ll use the custom Kepler solver that is implemented as part of exoplanet and fit the publicly available radial velocity observations of the famous exoplanetary system 51 Peg using PyMC.
First, we need to download the data from the exoplanet archive:
import requests
import pandas as pd
import matplotlib.pyplot as plt
# Download the dataset from the Exoplanet Archive:
url = "https://exoplanetarchive.ipac.caltech.edu/data/ExoData/0113/0113357/data/UID_0113357_RVC_001.tbl"
r = requests.get(url)
if r.status_code != requests.codes.ok:
r.raise_for_status()
data = np.array(
[
l.split()
for l in r.text.splitlines()
if not l.startswith("\\") and not l.startswith("|")
],
dtype=float,
)
t, rv, rv_err = data.T
t -= np.mean(t)
# Plot the observations "folded" on the published period:
# Butler et al. (2006) https://arxiv.org/abs/astro-ph/0607493
lit_period = 4.230785
plt.errorbar(
(t % lit_period) / lit_period, rv, yerr=rv_err, fmt=".k", capsize=0
)
plt.xlim(0, 1)
plt.ylim(-110, 110)
plt.annotate(
"period = {0:.6f} days".format(lit_period),
xy=(1, 0),
xycoords="axes fraction",
xytext=(-5, 5),
textcoords="offset points",
ha="right",
va="bottom",
fontsize=12,
)
plt.ylabel("radial velocity [m/s]")
_ = plt.xlabel("phase")
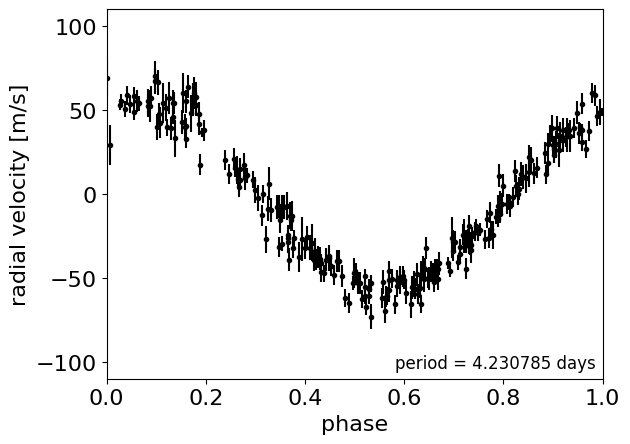
Now, here’s the implementation of a radial velocity model in PyMC. Some of this will look familiar after the Hello World example, but things are a bit more complicated now. Take a minute to take a look through this and see if you can follow it. There’s a lot going on, so I want to point out a few things to pay attention to:
All of the mathematical operations (for example
expandsqrt) are being performed using PyTensor instead of NumPy.All of the parameters have initial guesses provided. This is an example where this makes a big difference because some of the parameters (like period) are very tightly constrained.
Some of the lines are wrapped in
Deterministicdistributions. This can be useful because it allows us to track values as the chain progresses even if they’re not parameters. For example, after sampling, we will have a sample forbkg(the background RV trend) for each step in the chain. This can be especially useful for making plots of the results.Similarly, at the end of the model definition, we compute the RV curve for a single orbit on a fine grid. This can be very useful for diagnosing fits gone wrong.
For parameters that specify angles (like \(\omega\), called
win the model below), it can be inefficient to sample in the angle directly because of the fact that the value wraps around at \(2\pi\). Instead, it can be better to sample the unit vector specified by the angle or as a parameter in a unit disk, when combined with eccentricity. There are some helper functions likeexoplanet.distributions.angle()andexoplanet.distributions.unit_disk()to help with this.
import pytensor.tensor as pt
import exoplanet as xo
with pm.Model() as model:
# Parameters
logK = pm.Uniform(
"logK",
lower=0,
upper=np.log(200),
initval=np.log(0.5 * (np.max(rv) - np.min(rv))),
)
logP = pm.Uniform(
"logP", lower=0, upper=np.log(10), initval=np.log(lit_period)
)
phi = pm.Uniform("phi", lower=0, upper=2 * np.pi, initval=0.1)
# Parameterize the eccentricity using:
# h = sqrt(e) * sin(w)
# k = sqrt(e) * cos(w)
h, k = xo.unit_disk("h", "k", initval=np.array([0.01, 0.01]))
e = pm.Deterministic("e", h**2 + k**2)
w = pm.Deterministic("w", pt.arctan2(k, h))
rv0 = pm.Normal("rv0", mu=0.0, sigma=10.0, initval=0.0)
rvtrend = pm.Normal("rvtrend", mu=0.0, sigma=10.0, initval=0.0)
# Deterministic transformations
n = 2 * np.pi * pt.exp(-logP)
P = pm.Deterministic("P", pt.exp(logP))
K = pm.Deterministic("K", pt.exp(logK))
cosw = pt.cos(w)
sinw = pt.sin(w)
t0 = (phi + w) / n
# The RV model
bkg = pm.Deterministic("bkg", rv0 + rvtrend * t / 365.25)
M = n * t - (phi + w)
# This is the line that uses the custom Kepler solver
f = xo.orbits.get_true_anomaly(M, e + pt.zeros_like(M))
rvmodel = pm.Deterministic(
"rvmodel", bkg + K * (cosw * (pt.cos(f) + e) - sinw * pt.sin(f))
)
# Condition on the observations
pm.Normal("obs", mu=rvmodel, sigma=rv_err, observed=rv)
# Compute the phased RV signal
phase = np.linspace(0, 1, 500)
M_pred = 2 * np.pi * phase - (phi + w)
f_pred = xo.orbits.get_true_anomaly(M_pred, e + pt.zeros_like(M_pred))
rvphase = pm.Deterministic(
"rvphase", K * (cosw * (pt.cos(f_pred) + e) - sinw * pt.sin(f_pred))
)
In this case, I’ve found that it is useful to first optimize the parameters to find the “maximum a posteriori” (MAP) parameters and then start the sampler from there.
This is useful here because MCMC is not designed to find the maximum of the posterior; it’s just meant to sample the shape of the posterior.
The performance of all MCMC methods can be really bad when the initialization isn’t good (especially when some parameters are very well-constrained).
To find the maximum a posteriori parameters using PyMC, you can use the find_MAP function:
with model:
map_params = pm.find_MAP()
/home/docs/checkouts/readthedocs.org/user_builds/exoplanet/envs/latest/lib/python3.10/site-packages/rich/live.py:23
1: UserWarning: install "ipywidgets" for Jupyter support
warnings.warn('install "ipywidgets" for Jupyter support')
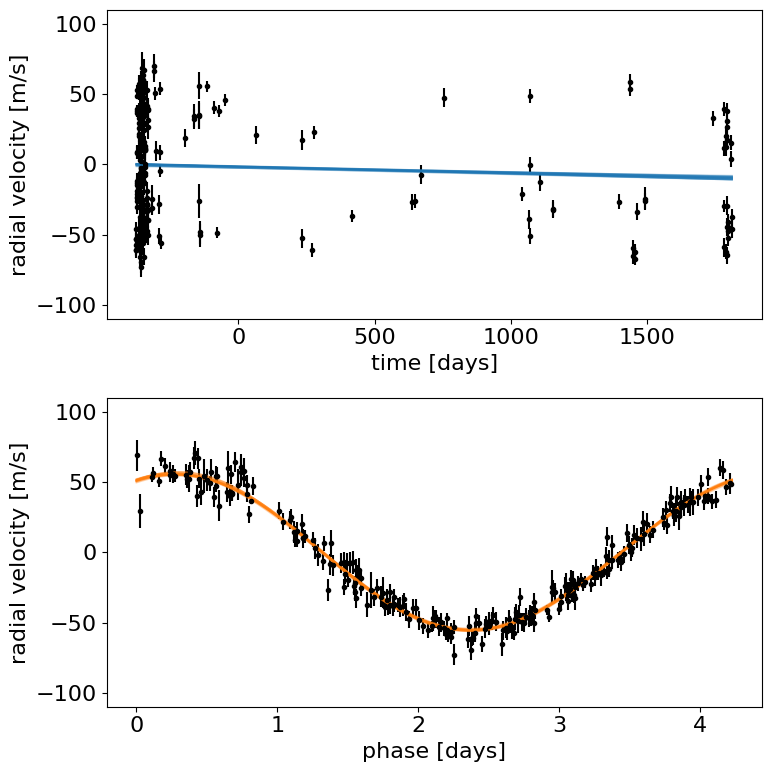
Let’s make a plot to check that this initialization looks reasonable. In the top plot, we’re looking at the RV observations as a function of time with the initial guess for the long-term trend overplotted in blue. In the lower panel, we plot the “folded” curve where we have wrapped the observations onto the best-fit period and the prediction for a single overplotted in orange. If this doesn’t look good, try adjusting the initial guesses for the parameters and see if you can get a better fit.
Exercise: Try changing the initial guesses for the parameters (as specified by the initval argument) and see how sensitive the results are to these values. Are there some parameters that are less important? Why is this?
fig, axes = plt.subplots(2, 1, figsize=(8, 8))
period = map_params["P"]
ax = axes[0]
ax.errorbar(t, rv, yerr=rv_err, fmt=".k")
ax.plot(t, map_params["bkg"], color="C0", lw=1)
ax.set_ylim(-110, 110)
ax.set_ylabel("radial velocity [m/s]")
ax.set_xlabel("time [days]")
ax = axes[1]
ax.errorbar(t % period, rv - map_params["bkg"], yerr=rv_err, fmt=".k")
ax.plot(phase * period, map_params["rvphase"], color="C1", lw=1)
ax.set_ylim(-110, 110)
ax.set_ylabel("radial velocity [m/s]")
ax.set_xlabel("phase [days]")
plt.tight_layout()
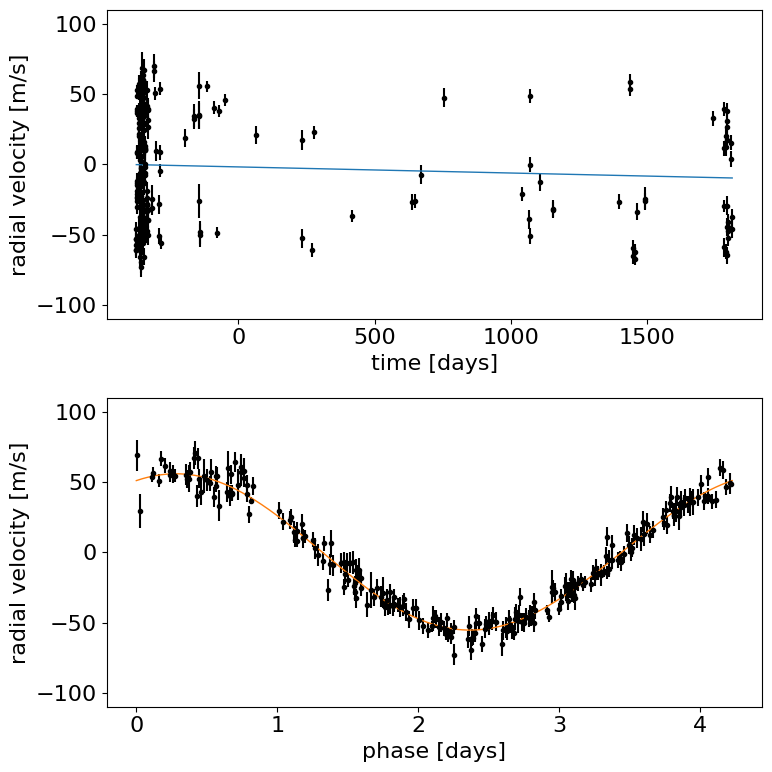
Now let’s sample the posterior starting from our MAP estimate:
with model:
trace = pm.sample(
draws=1000,
tune=1000,
initvals=map_params,
chains=2,
cores=2,
target_accept=0.95,
init="adapt_full",
)
Auto-assigning NUTS sampler...
Initializing NUTS using adapt_full...
/home/docs/checkouts/readthedocs.org/user_builds/exoplanet/envs/latest/lib/python3.10/site-packages/pymc/step_methods/hmc/quadpotential.py:627: UserWarning: QuadPotentialFullAdapt is an experimental feature
warnings.warn("QuadPotentialFullAdapt is an experimental feature")
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [logK, logP, phi, h, __k_unit_disk, rv0, rvtrend]
/home/docs/checkouts/readthedocs.org/user_builds/exoplanet/envs/latest/lib/python3.10/site-packages/rich/live.py:23
1: UserWarning: install "ipywidgets" for Jupyter support
warnings.warn('install "ipywidgets" for Jupyter support')
Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 44 seconds.
We recommend running at least 4 chains for robust computation of convergence diagnostics
As above, it’s always a good idea to take a look at the summary statistics for the chain. If everything went as planned, there should be more than 1000 effective samples per chain and the Rhat values should be close to 1. (Not too bad for about 30 seconds of run time!)
az.summary(
trace,
var_names=["logK", "logP", "phi", "e", "w", "rv0", "rvtrend"],
)
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | |
|---|---|---|---|---|---|---|---|---|---|
| logK | 4.019 | 0.010 | 4.003 | 4.039 | 0.000 | 0.000 | 2263.0 | 1391.0 | 1.00 |
| logP | 1.442 | 0.000 | 1.442 | 1.442 | 0.000 | 0.000 | 2056.0 | 1484.0 | 1.00 |
| phi | 0.397 | 0.010 | 0.379 | 0.416 | 0.000 | 0.000 | 2598.0 | 1168.0 | 1.01 |
| e | 0.010 | 0.008 | 0.000 | 0.024 | 0.000 | 0.000 | 1928.0 | 1765.0 | 1.00 |
| w | 0.579 | 1.340 | -2.429 | 2.865 | 0.032 | 0.023 | 1696.0 | 1640.0 | 1.00 |
| rv0 | -1.807 | 0.389 | -2.503 | -1.018 | 0.008 | 0.006 | 2163.0 | 1453.0 | 1.00 |
| rvtrend | -1.590 | 0.191 | -1.957 | -1.247 | 0.004 | 0.003 | 2571.0 | 1475.0 | 1.00 |
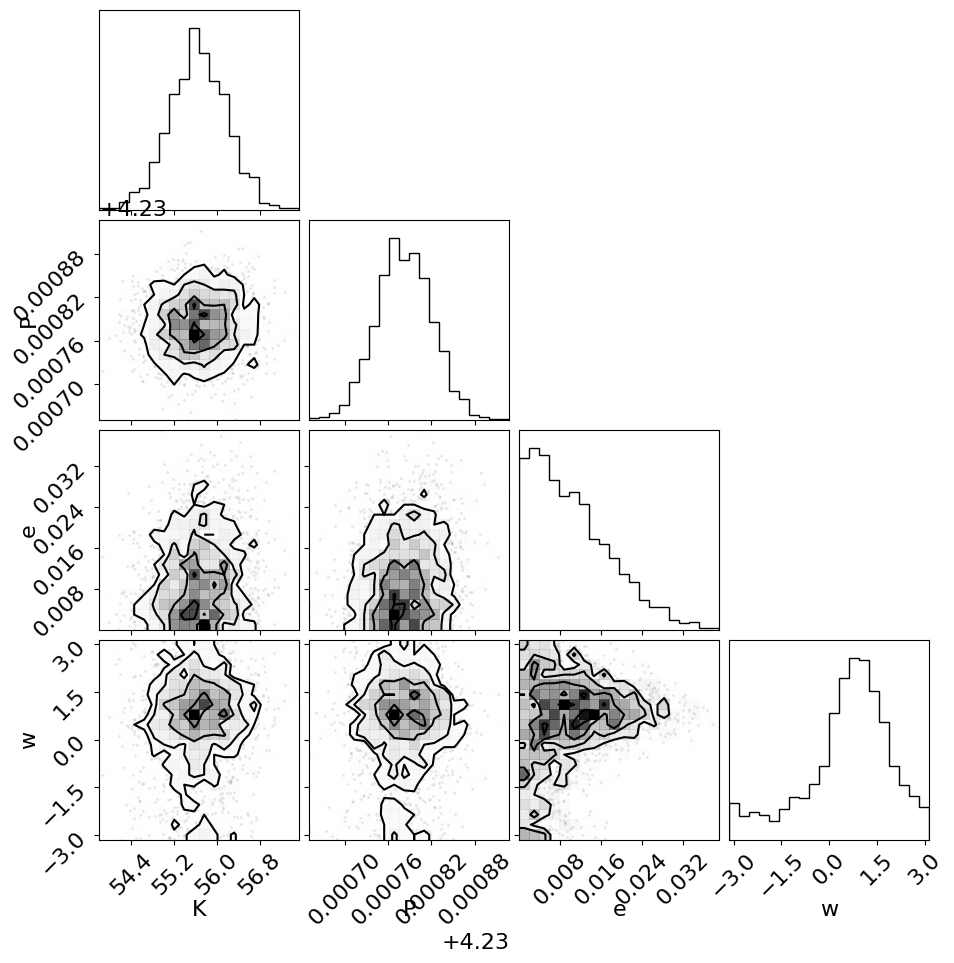
Similarly, we can make the corner plot again for this model.
_ = corner.corner(trace, var_names=["K", "P", "e", "w"])
Finally, the last plot that we’ll make here is of the posterior predictive density. In this case, this means that we want to look at the distribution of predicted models that are consistent with the data. As above, the top plot shows the raw observations as black error bars and the RV trend model is overplotted in blue. But, this time, the blue line is actually composed of 25 lines that are samples from the posterior over trends that are consistent with the data. In the bottom panel, the orange lines indicate the same 25 posterior samples for the RV curve of one orbit.
fig, axes = plt.subplots(2, 1, figsize=(8, 8))
period = map_params["P"]
ax = axes[0]
ax.errorbar(t, rv, yerr=rv_err, fmt=".k")
ax.set_ylabel("radial velocity [m/s]")
ax.set_xlabel("time [days]")
ax = axes[1]
ax.errorbar(t % period, rv - map_params["bkg"], yerr=rv_err, fmt=".k")
ax.set_ylabel("radial velocity [m/s]")
ax.set_xlabel("phase [days]")
bkg = trace.posterior["bkg"].values
rvphase = trace.posterior["rvphase"].values
for ind in np.random.randint(np.prod(bkg.shape[:2]), size=25):
i = np.unravel_index(ind, bkg.shape[:2])
axes[0].plot(t, bkg[i], color="C0", lw=1, alpha=0.3)
axes[1].plot(phase * period, rvphase[i], color="C1", lw=1, alpha=0.3)
axes[0].set_ylim(-110, 110)
axes[1].set_ylim(-110, 110)
plt.tight_layout()