Note

This tutorial was generated from an IPython notebook that can be downloaded here.

Scalable Gaussian processes in PyMC3

PyMC3 has support for Gaussian Processes (GPs), but this implementation is too slow for many applications in time series astrophysics. So exoplanet comes with an implementation of scalable GPs powered by celerite. More information about the algorithm can be found in the celerite docs and in the papers (Paper 1 and Paper 2), but this tutorial will give a hands on demo of how to use celerite in PyMC3.

Note

For the best results, we generally recommend the use of the exoplanet.gp.terms.SHOTerm, exoplanet.gp.terms.Matern32Term, and exoplanet.gp.terms.RotationTerm “terms” because the other terms tend to have unphysical behavior at high frequency.

Let’s start with the quickstart demo from the celerite docs. We’ll fit the following simulated dataset using the sum of two exoplanet.gp.terms.SHOTerm objects.

First, generate the simulated data:

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)

t = np.sort(np.append(
    np.random.uniform(0, 3.8, 57),
    np.random.uniform(5.5, 10, 68),
))  # The input coordinates must be sorted
yerr = np.random.uniform(0.08, 0.22, len(t))
y = 0.2 * (t-5) + np.sin(3*t + 0.1*(t-5)**2) + yerr * np.random.randn(len(t))

true_t = np.linspace(0, 10, 5000)
true_y = 0.2 * (true_t-5) + np.sin(3*true_t + 0.1*(true_t-5)**2)

plt.errorbar(t, y, yerr=yerr, fmt=".k", capsize=0, label="data")
plt.plot(true_t, true_y, "k", lw=1.5, alpha=0.3, label="truth")
plt.legend(fontsize=12)
plt.xlabel("t")
plt.ylabel("y")
plt.xlim(0, 10)
plt.ylim(-2.5, 2.5);
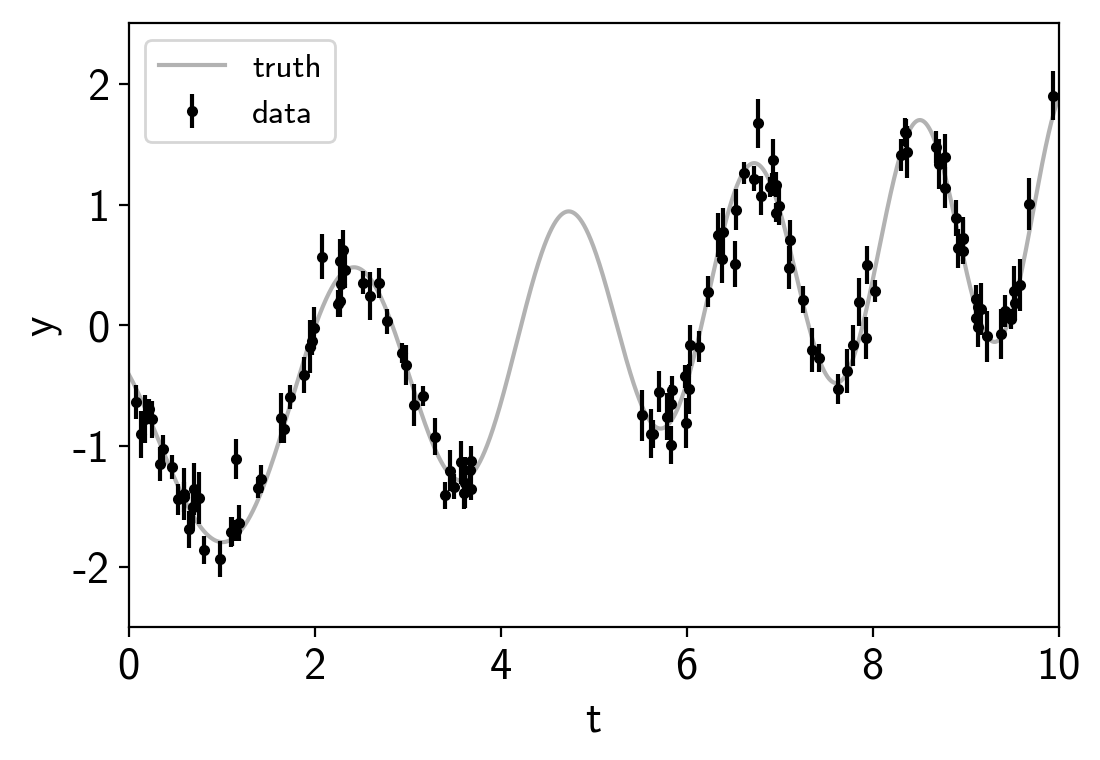
../../_images/gp_5_0.png

This plot shows the simulated data as black points with error bars and the true function is shown as a gray line.

Now let’s build the PyMC3 model that we’ll use to fit the data. We can see that there’s some roughly periodic signal in the data as well as a longer term trend. To capture these two features, we will model this as a mixture of two stochastically driven simple harmonic oscillators (SHO) with the power spectrum:

\[S(\omega) = \sqrt{\frac{2}{\pi}}\frac{S_1\,{\omega_1}^4}{(\omega^2 - {\omega_1}^2)^2 + 2\,{\omega_1}^2\,\omega^2} + \sqrt{\frac{2}{\pi}}\frac{S_2\,{\omega_2}^4}{(\omega^2 - {\omega_2}^2)^2 + {\omega_2}^2\,\omega^2/Q^2}\]

The first term is exoplanet.gp.terms.SHOterm with \(Q=1/\sqrt{2}\) and the second is regular exoplanet.gp.terms.SHOterm. This model has 5 free parameters (\(S_1\), \(\omega_1\), \(S_2\), \(\omega_2\), and \(Q\)) and they must all be positive so we’ll fit for the log of each parameter. Using exoplanet, this is how you would build this model, choosing more or less arbitrary initial values for the parameters.

import pymc3 as pm
import theano.tensor as tt
from exoplanet.gp import terms, GP

with pm.Model() as model:

    logS1 = pm.Normal("logS1", mu=0.0, sd=15.0, testval=np.log(np.var(y)))
    logw1 = pm.Normal("logw1", mu=0.0, sd=15.0, testval=np.log(3.0))
    logS2 = pm.Normal("logS2", mu=0.0, sd=15.0, testval=np.log(np.var(y)))
    logw2 = pm.Normal("logw2", mu=0.0, sd=15.0, testval=np.log(3.0))
    logQ = pm.Normal("logQ", mu=0.0, sd=15.0, testval=0)

    # Set up the kernel an GP
    kernel = terms.SHOTerm(log_S0=logS1, log_w0=logw1, Q=1.0/np.sqrt(2))
    kernel += terms.SHOTerm(log_S0=logS2, log_w0=logw2, log_Q=logQ)
    gp = GP(kernel, t, yerr**2)

    # Add a custom "potential" (log probability function) with the GP likelihood
    pm.Potential("gp", gp.log_likelihood(y))

A few comments here:

  1. The term interface in exoplanet only accepts keyword arguments with names given by the parameter_names property of the term. But it will also interpret keyword arguments with the name prefaced by log_ to be the log of the parameter. For example, in this case, we used log_S0 as the parameter for each term, but S0=tt.exp(log_S0) would have been equivalent. This is useful because many of the parameters are required to be positive so fitting the log of those parameters is often best.
  2. The third argument to the exoplanet.gp.GP constructor should be the variance to add along the diagonal, not the standard deviation as in the original celerite implementation.
  3. Finally, the exoplanet.gp.GP constructor takes an optional argument J which specifies the width of the problem if it is known at compile time. Just to be confusing, this is actually two times the J from the celerite paper. There are various technical reasons why this is difficult to work out in general and this code will always work if you don’t provide a value for J, but you can get much better performance (especially for small J) if you know what it will be for your problem. In general, most terms cost J=2 with the exception of a exoplanet.gp.terms.RealTerm (which costs J=1) and a exoplanet.gp.terms.RotationTerm (which costs J=4).

To start, let’s fit for the maximum a posteriori (MAP) parameters and look the the predictions that those make.

with model:
    map_soln = pm.find_MAP(start=model.test_point)

logp = -1.651, ||grad|| = 0.05773: 100%|██████████| 48/48 [00:00<00:00, 902.22it/s]

We’ll use the exoplanet.utils.eval_in_model() function to evaluate the MAP GP model.

from exoplanet.utils import eval_in_model

with model:
    mu, var = eval_in_model(gp.predict(true_t, return_var=True), map_soln)

plt.errorbar(t, y, yerr=yerr, fmt=".k", capsize=0, label="data")
plt.plot(true_t, true_y, "k", lw=1.5, alpha=0.3, label="truth")

# Plot the prediction and the 1-sigma uncertainty
sd = np.sqrt(var)
art = plt.fill_between(true_t, mu+sd, mu-sd, color="C1", alpha=0.3)
art.set_edgecolor("none")
plt.plot(true_t, mu, color="C1", label="prediction")

plt.legend(fontsize=12)
plt.xlabel("t")
plt.ylabel("y")
plt.xlim(0, 10)
plt.ylim(-2.5, 2.5);
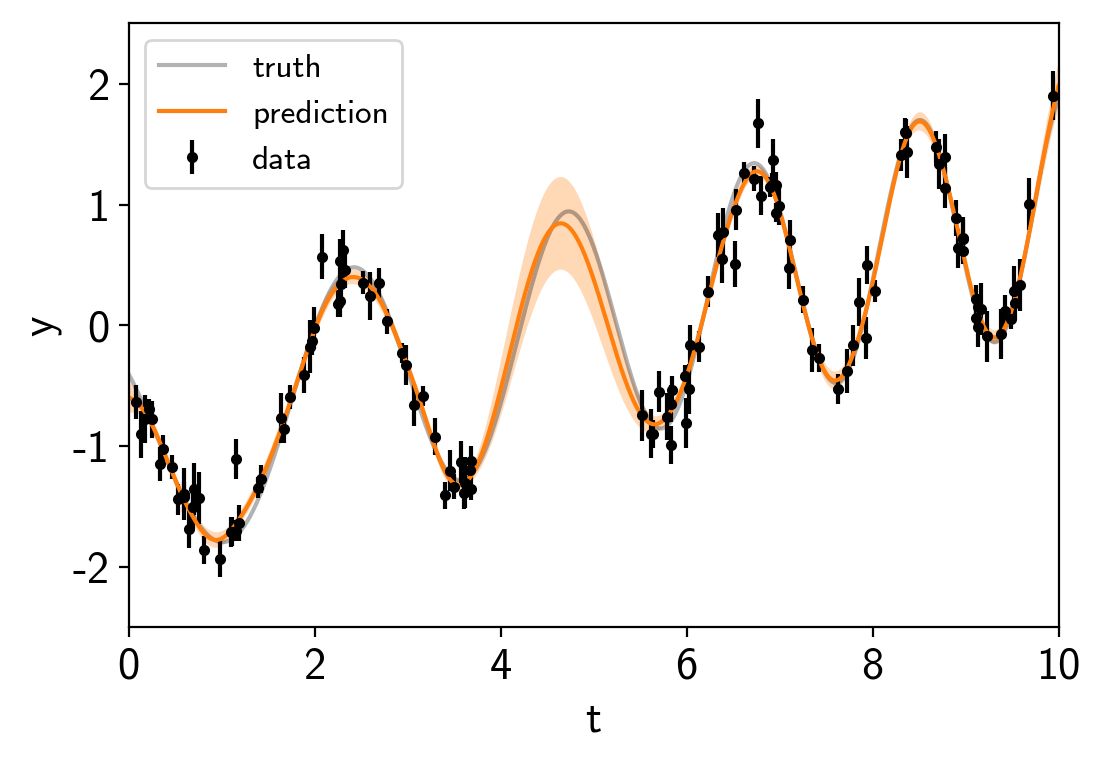
../../_images/gp_12_0.png

Now we can sample this model using PyMC3. There are strong covariances between the parameters so we’ll use the custom exoplanet.sampling.TuningSchedule to fit for these covariances during burn-in.

from exoplanet.sampling import PyMC3Sampler

sampler = PyMC3Sampler()

with model:
    burnin = sampler.tune(tune=1000, chains=2, start=map_soln)
    trace = sampler.sample(draws=2000, chains=2)

Sampling 2 chains: 100%|██████████| 154/154 [00:06<00:00, 22.31draws/s]
Sampling 2 chains: 100%|██████████| 54/54 [00:01<00:00, 35.27draws/s]
Sampling 2 chains: 100%|██████████| 104/104 [00:00<00:00, 143.38draws/s]
Sampling 2 chains: 100%|██████████| 204/204 [00:01<00:00, 181.87draws/s]
Sampling 2 chains: 100%|██████████| 404/404 [00:02<00:00, 199.49draws/s]
Sampling 2 chains: 100%|██████████| 1104/1104 [00:04<00:00, 268.79draws/s]
Multiprocess sampling (2 chains in 4 jobs)
NUTS: [logQ, logw2, logS2, logw1, logS1]
Sampling 2 chains: 100%|██████████| 4100/4100 [00:18<00:00, 218.44draws/s]
There were 3 divergences after tuning. Increase target_accept or reparameterize.
The acceptance probability does not match the target. It is 0.8813938336202713, but should be close to 0.8. Try to increase the number of tuning steps.
There were 7 divergences after tuning. Increase target_accept or reparameterize.
The acceptance probability does not match the target. It is 0.8804565191475396, but should be close to 0.8. Try to increase the number of tuning steps.

Now we can compute the standard PyMC3 convergence statistics (using pymc3.summary) and make a trace plot (using pymc3.traceplot).

pm.traceplot(trace)
pm.summary(trace)
mean sd mc_error hpd_2.5 hpd_97.5 n_eff Rhat
logS1 4.725402 3.664236 0.094171 -0.870037 12.141039 1376.010207 1.000167
logw1 -2.378219 1.335232 0.033231 -5.144494 -0.015903 1436.884278 0.999800
logS2 -4.082574 0.486063 0.012238 -4.936555 -3.088807 1469.672700 1.000088
logw2 1.130917 0.052122 0.001142 1.023500 1.224969 2026.219887 1.000202
logQ 2.918510 1.241179 0.033231 0.916001 5.434840 1164.144845 0.999833
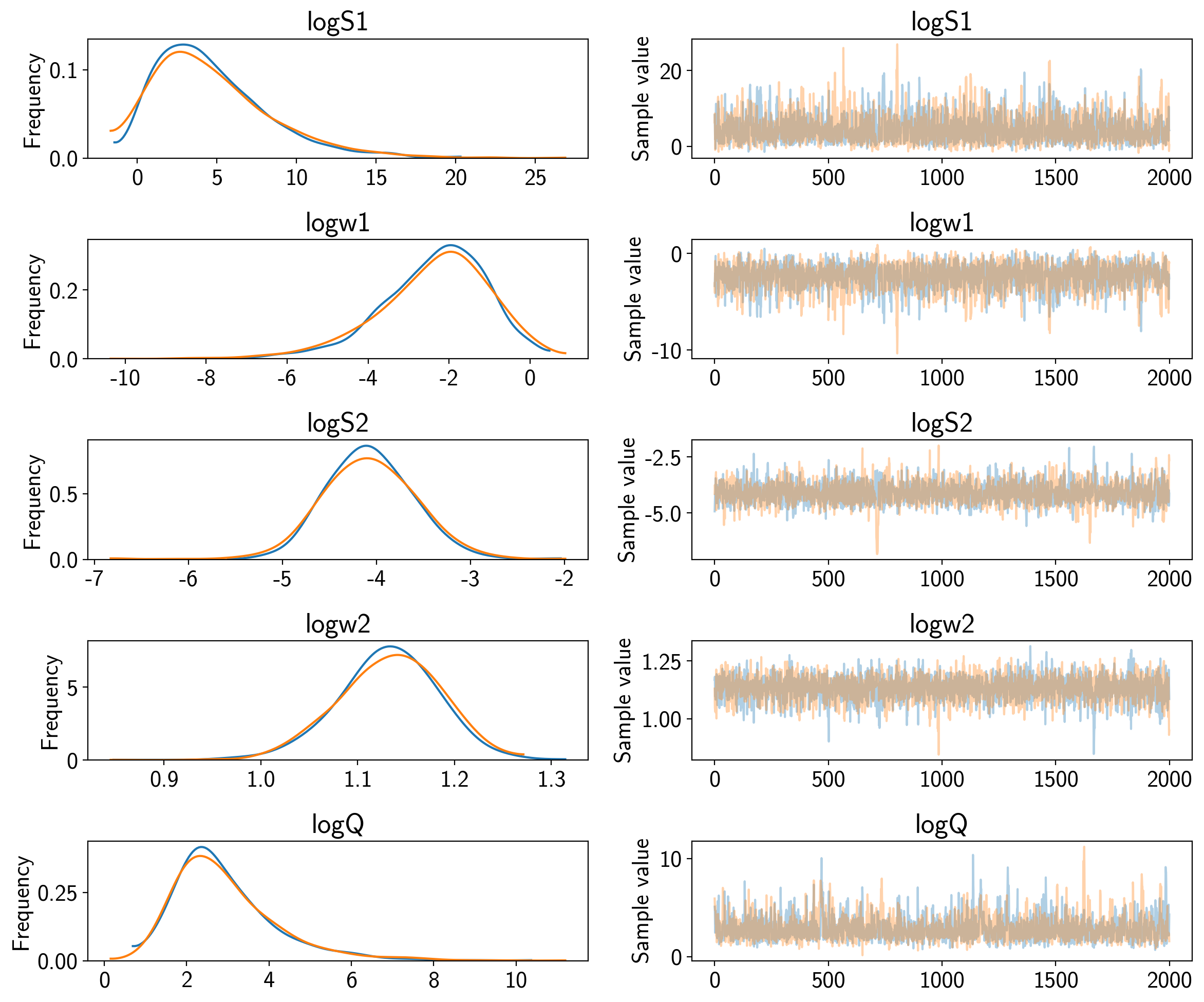
../../_images/gp_16_1.png

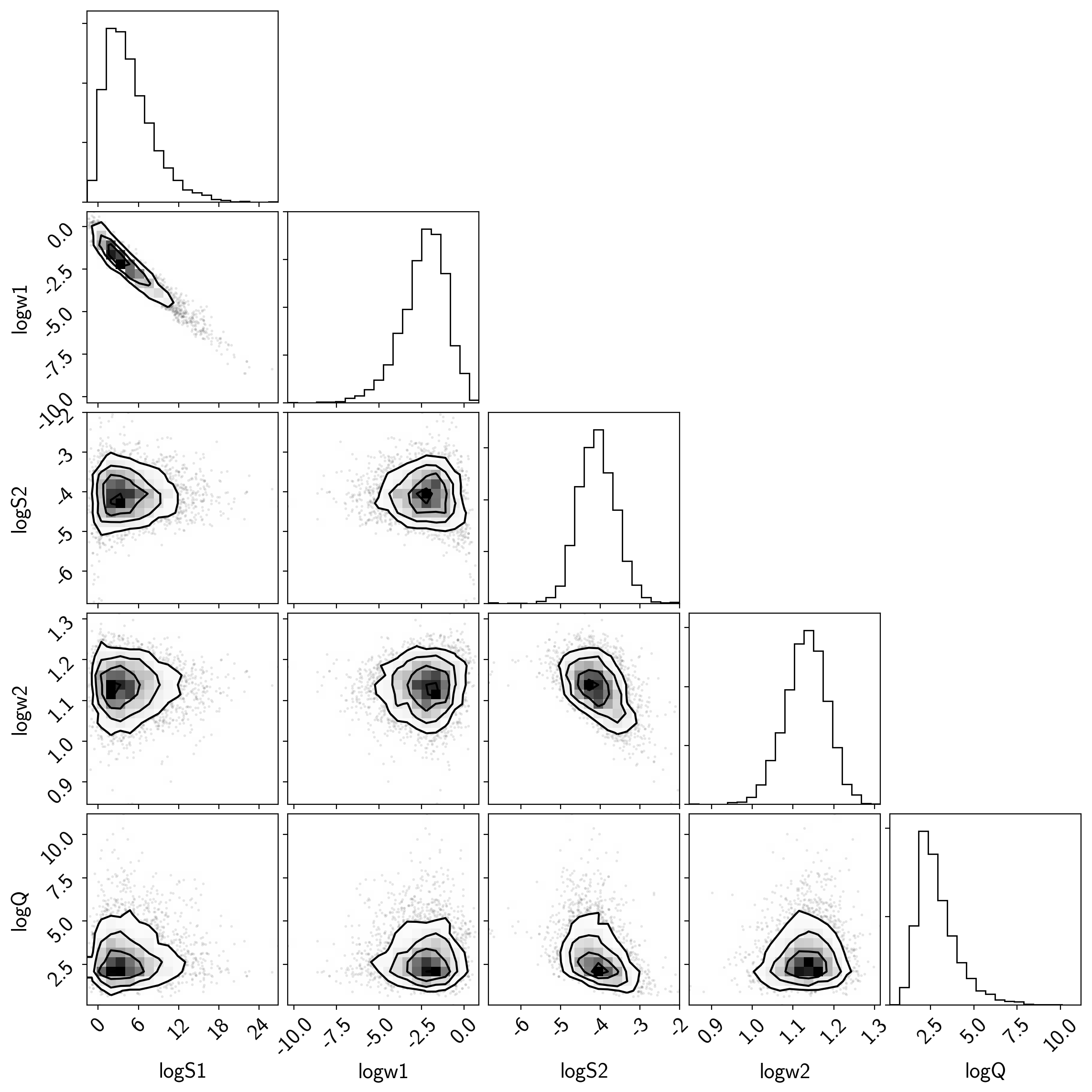
That all looks pretty good, but I like to make two other results plots: (1) a corner plot and (2) a posterior predictive plot.

The corner plot is easy using pymc3.trace_to_dataframe and I find it useful for understanding the covariances between parameters when debugging.

import corner
samples = pm.trace_to_dataframe(trace)
corner.corner(samples);
../../_images/gp_18_0.png

The “posterior predictive” plot that I like to make isn’t the same as a “posterior predictive check” (which can be a good thing to do too). Instead, I like to look at the predictions of the model in the space of the data. We could have saved these predictions using a pymc3.Deterministic distribution, but that adds some overhead to each evaluation of the model so instead, we can use exoplanet.utils.get_samples_from_trace() to loop over a few random samples from the chain and then the exoplanet.utils.eval_in_model() function to evaluate the prediction just for those samples.

from exoplanet.utils import get_samples_from_trace

# Generate 50 realizations of the prediction sampling randomly from the chain
N_pred = 50
pred_mu = np.empty((N_pred, len(true_t)))
pred_var = np.empty((N_pred, len(true_t)))
with model:
    pred = gp.predict(true_t, return_var=True)
    for i, sample in enumerate(get_samples_from_trace(trace, size=N_pred)):
        pred_mu[i], pred_var[i] = eval_in_model(pred, sample)

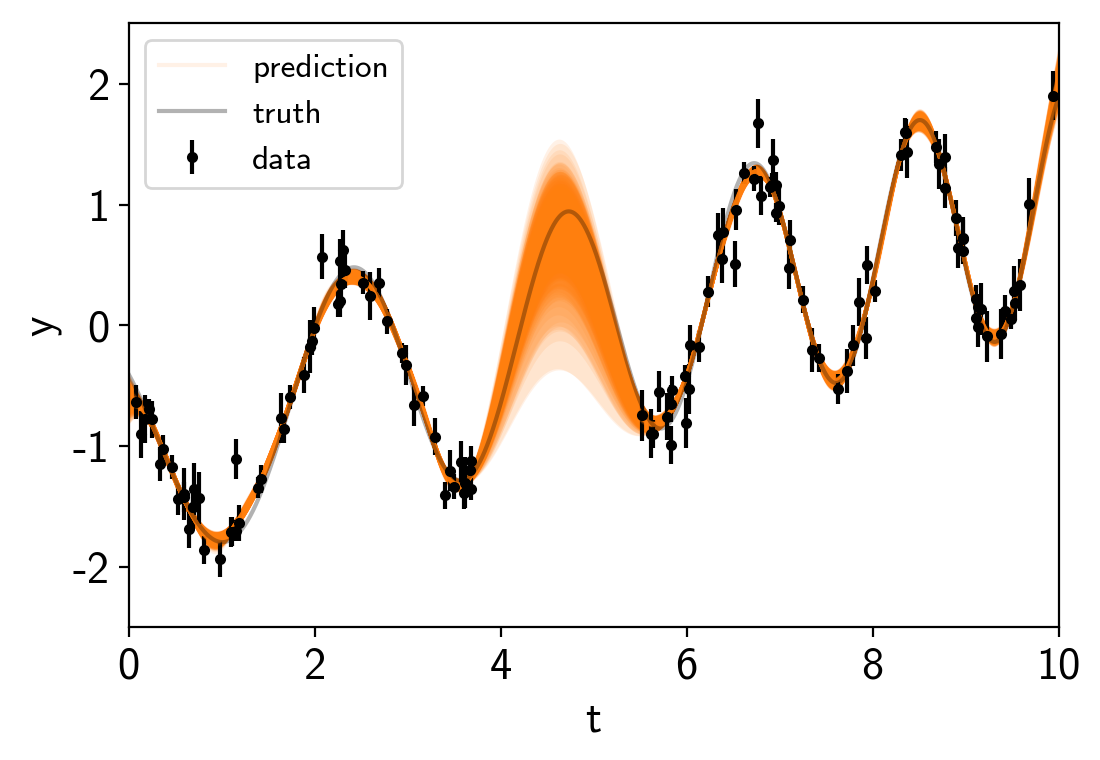
# Plot the predictions
for i in range(len(pred_mu)):
    mu = pred_mu[i]
    sd = np.sqrt(pred_var[i])
    label = None if i else "prediction"
    art = plt.fill_between(true_t, mu+sd, mu-sd, color="C1", alpha=0.1)
    art.set_edgecolor("none")
    plt.plot(true_t, mu, color="C1", label=label, alpha=0.1)

plt.errorbar(t, y, yerr=yerr, fmt=".k", capsize=0, label="data")
plt.plot(true_t, true_y, "k", lw=1.5, alpha=0.3, label="truth")
plt.legend(fontsize=12)
plt.xlabel("t")
plt.ylabel("y")
plt.xlim(0, 10)
plt.ylim(-2.5, 2.5);
../../_images/gp_20_0.png